Question

【题目】设全集U=R，集合A={x|2x-1≥1}，B={x|x2-4x-5＜0}．

（Ⅰ）求A∩B，（UA）∪（UB）；

（Ⅱ）设集合C={x|m+1＜x＜2m-1}，若B∩C=C，求实数m的取值范围．

Answer 1

【答案】 （Ⅰ）{x|x＜1或x≥5}，（Ⅱ）（-∞，3] .

【解析】

（Ⅰ）求出集合A，B，由此能出A∩B，（UA）∪（UB）．

（Ⅱ）由集合C＝{x|m+1＜x＜2m﹣1}，B∩C＝C，得CB，当C＝时，2m﹣1＜m+1，当C≠时，由CB得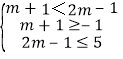，由此能求出m的取值范围．

解：（Ⅰ）∵全集U=R，集合A={x|2x-1≥1}={x|x≥1}，

B={x|x2-4x-5＜0}={x|-1＜x＜5}

∴A∩B={x|1≤x＜5}，

（CUA）∪（CUB）={x|x＜1或x≥5}

（Ⅱ）∵集合C={x|m+1＜x＜2m-1}，B∩C=C，

∴CB，

当C=时，

解得

当C≠时，由CB得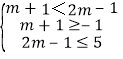，解得：2＜m≤3

综上所述：m的取值范围是（-∞，3]