练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知定义在区间（﹣1，1）上的偶函数f（x），在（0，1）上为增函数，f（a﹣2）﹣f（4﹣a2）＜0，求实数a的取值范围．

    【答案】解：∵偶函数f（x），在（0，1）上为增函数，
    ∴在（﹣1，0）上为减函数，
    若f（a﹣2）﹣f（4﹣a2）＜0，
    则f（a﹣2）＜f（4﹣a2）
    则|a﹣2|＜|4﹣a2|＜1且a﹣2≠0
    解得：a∈（﹣ ，﹣ ），
    故实数a的取值范围是（﹣ ，﹣ ）
    【解析】由已知中定义在区间（﹣1，1）上的偶函数f（x），在（0，1）上为增函数，我们可判断出函数的单调性，进而将抽象不等式f（a﹣2）﹣f（4﹣a2）＜0，化为绝对值不等式，平方法解答可得到答案．
    【考点精析】利用奇偶性与单调性的综合对题目进行判断即可得到答案，需要熟知奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设 个正数 满足 （ 且 ）．
    （1）当 时，证明： ；
    （2）当 时，不等式 也成立，请你将其推广到 （ 且 ）个正数 的情形，归纳出一般性的结论并用数学归纳法证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数y=f（x）在R上可导且满足不等式xf′（x）+f（x）＞0恒成立，且常数a，b满足a＞b，则下列不等式一定成立的是（ ）
    A.af（a）＞bf（b）
    B.af（b）＞bf（a）
    C.af（a）＜bf（b）
    D.af（b）＜bf（a）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

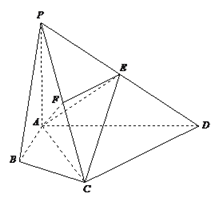
    【题目】四棱锥P－ABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，PA⊥平面ABCD，

    E为PD的中点，PA＝2AB＝2．

    （1）若F为PC的中点，求证PC⊥平面AEF；

    （2）求二面角的平面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|x2﹣3x+2=0}，B={x|x2﹣mx+m﹣1=0}若A∪B=A，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

    已知函数， ,且函数在处的切线平行于直线．

    （Ⅰ）实数的值；（Ⅱ）若在（）上存在一点，使得成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学在高二年级开设大学选修课程《线性代数》，共有名同学选修，其中男同学名，女同学名.为了对这门课程的教学效果进行评估，学校按性别采取分层抽样的方法抽取人进行考核.

    （1）求抽取的人中男、女同学的人数；

    （2）考核前，评估小组打算从选出的中随机选出名同学进行访谈，求选出的两名同学中恰有一名女同学的概率；

    （3）考核分答辩和笔试两项. 位同学的笔试成绩分别为；结合答辩情况，他们的考核成绩分别为.这位同学笔试成绩与考核成绩的方差分别记为，试比较和的大小.（只需写出结论）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f(x)=x3-3ax2+3bx的图像与直线12x+y-1=0相切于点（1，－11）。
    （1）求a，b的值；
    （2）讨论函数f(x)的单调性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设命题p：函数f(x)＝lg(ax2－x＋ a)的定义域为R；命题q：不等式3x－9x＜a对一切正实数均成立．如果命题“p∨q”为真命题，“p∧q”为假命题，求实数a的取值范围( )．
    A.0≤a＜1
    B.0≤a
    C.a≤1
    D.0≤a≤1

    查看答案和解析>>

    同步练习册答案