
如图,要计算西湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两点,现测得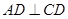 ,
,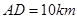 ,
,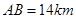 ,
,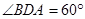 ,
,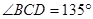 ,求两景点B与C的距离.
,求两景点B与C的距离.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A- sin A)cos B=0.
sin A)cos B=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知△ABC中,内角A,B,C的对边分别为a,b,c,其中a=2,c= .
.
(1)若sinC=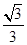 ,求sinA的值;
,求sinA的值;
(2)设f(C)= sinCcosC-cos2C,求f(C)的取值范围.
sinCcosC-cos2C,求f(C)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图, 、
、 是两个小区所在地,
是两个小区所在地, 、
、 到一条公路
到一条公路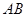 的垂直距离分别为
的垂直距离分别为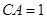
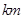 ,
,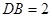
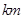 ,
,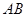 两端之间的距离为
两端之间的距离为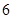
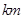 .
.
(1)某移动公司将在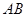 之间找一点
之间找一点 ,在
,在 处建造一个信号塔,使得
处建造一个信号塔,使得 对
对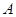 、
、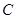 的张角与
的张角与 对
对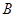 、
、 的张角相等,试确定点
的张角相等,试确定点 的位置.
的位置.
(2)环保部门将在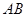 之间找一点
之间找一点 ,在
,在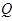 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得 对
对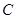 、
、 所张角最大,试确定点
所张角最大,试确定点 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,A,B是海面上位于东西方向相距5(3+ )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com