
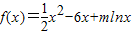 的一个极值点.
的一个极值点.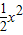 +(6-b)x+2(a>0),G(x)=f(x)+g(x),若G(x)=0有两个不同零点x1,x2,且
+(6-b)x+2(a>0),G(x)=f(x)+g(x),若G(x)=0有两个不同零点x1,x2,且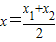 ,试探究G′(x)值的符号.
,试探究G′(x)值的符号. ,于是G′(x)可用x1,x2表示,构造关于t=
,于是G′(x)可用x1,x2表示,构造关于t=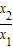 的函数,按0<x1<x2,0<x2<x1两种情况进行讨论可判断G′(x)的符号;
的函数,按0<x1<x2,0<x2<x1两种情况进行讨论可判断G′(x)的符号;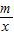 ,
,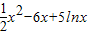 (x>0),
(x>0),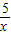 =
=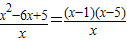 ,
,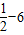 =-
=-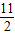 ,
,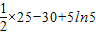 =-
=-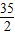 +5ln5,
+5ln5,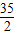 +5ln5<n<-
+5ln5<n<-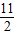 ;
;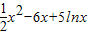 +(-5-a)lnx+
+(-5-a)lnx+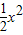 +(6-b)x+2=x2+2-alnx-bx有两个零点x1,x2,
+(6-b)x+2=x2+2-alnx-bx有两个零点x1,x2,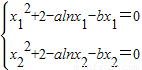 ,
,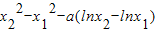 -b(x2-x1)=0,即
-b(x2-x1)=0,即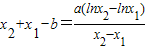 ,
,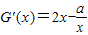 -b=
-b=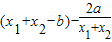
 -
-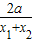 =
=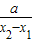 [ln
[ln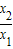 -
-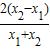 ]=
]=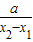 [ln
[ln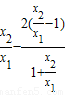 ],
], =t,则t>1,且G′(x)=
=t,则t>1,且G′(x)=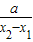 (lnt-
(lnt-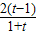 ).
).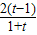 (t>1),
(t>1),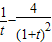 =
=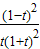 >0,
>0,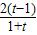 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.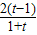 >0.
>0.

科目:高中数学 来源: 题型:
| x2 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| b |
| x |
| 3 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a2 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年崇文区统一练习一)(14分)
已知定义在R上的函数![]() ,其中a为常数.
,其中a为常数.
(I)若x=1是函数![]() 的一个极值点,求a的值;
的一个极值点,求a的值;
(II)若函数![]() 在区间(-1,0)上是增函数,求a的取值范围;
在区间(-1,0)上是增函数,求a的取值范围;
(III)若函数![]() ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com