Question

11．已知P是直线kx+4y-10=0（k＞0）上的动点，是圆C：x²+y²-2x+4y+4=0的两条切线，A，B是切点，C是圆心，若四边形PACB面积的最小值为$2\sqrt{2}$，则k的值为（　　）

• A． 3
• B． 2
• C． $\frac{1}{3}$
• D． $\frac{15}{2}$

Answer 1

分析 S_{四边形PACB}=S_△PAC+S_△PBC，当|PC|取最小值时，|PA|=|PB|取最小值，即S_△PAC=S_△PBC取最小值，此时，CP⊥l由此利用四边形PACB面积的最小值，即可得出结论．．

解答 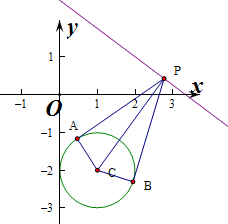解：圆的标准方程为（x-1）²+（y+2）²=1，
则圆心为C（1，-2），半径为1，
则直线与圆相离，如图，S四边形_PACB=S_△PAC+S_△PBC
而S_△PAC=$\frac{1}{2}$|PA|•|CA|=$\frac{1}{2}$|PA|，
S_△PBC=$\frac{1}{2}$|PB|•|CB|=|PB|，
又|PA|=|PB|=$\sqrt{|PC{|}^{2}-1}$，
∴当|PC|取最小值时，|PA|=|PB|取最小值，
即S_△PAC=S_△PBC取最小值，此时，CP⊥l，
四边形PACB面积的最小值为$2\sqrt{2}$，S_△PAC=S_△PBC=$\sqrt{2}$，
∴|PA|=2$\sqrt{2}$，∴|CP|=3，∴$\frac{|k-8-10|}{\sqrt{{k}^{2}+16}}$=3，
∵k＞0，∴k=3．
故选A．

点评 本题考查直线和圆的位置关系，解题时要认真审题，在解答过程中要合理地运用数形结合思想．