
 是奇函数,f(x)=lg(10x+1)+mx是偶函数.
是奇函数,f(x)=lg(10x+1)+mx是偶函数. ,若g(x)>h[lg(2a+1)]对任意x≥1恒成立,求实数a的取值范围.
,若g(x)>h[lg(2a+1)]对任意x≥1恒成立,求实数a的取值范围.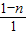 =0,解得n=1
=0,解得n=1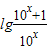 -mx=lg(10x+1)-x-mx=lg(10x+1)-(m+1)x
-mx=lg(10x+1)-x-mx=lg(10x+1)-(m+1)x ∴m+n=
∴m+n=
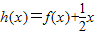 =lg(10x+1)
=lg(10x+1) 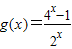 =2x-2-x
=2x-2-x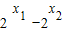 )
)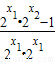 >0
>0
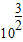 ,2a+1>0,2a+2>0,
,2a+1>0,2a+2>0, <a<5
<a<5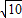 -1
-1 <a<5
<a<5 -1}
-1}

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
 是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.
是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆市西南师大附中高三(上)9月月考数学试卷(文科)(解析版) 题型:解答题
 是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.
是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.查看答案和解析>>
科目:高中数学 来源:2011年辽宁省重点高中协作体高考夺标预测数学试卷(2)(解析版) 题型:选择题
 (a>0),有下列四个命题:
(a>0),有下列四个命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com