练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】①线性回归方程对应的直线至少经过其样本数据点中的一个点；

    ②若两个变量的线性相关性越强，则相关系数的绝对值越接近于；

    ③在某项测量中，测量结果服从正态分布 ，若位于区域内的概率为，则位于区域内的概率为；

    ④对分类变量与的随机变量K2的观测值k来说，k越小，判断“与有关系”的把握越大．其中真命题的序号为( )

    A. ①④ B. ②④ C. ①③ D. ②③

    【答案】D

    【解析】对于①，因为线性回归方程是由最小二乘法计算出来的，所以它不一定经过其样本数据点，一定经过，故错误；对于②，根据随机变量的相关系数知，两个随机变量相关性越强，则相关系数的绝对值越接近于1，故正确；对于③，变量服从正态分布，则，故正确；对于④，随机变量的观测值越大，判断“与有关系”的把握越大，故错误.

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱中，，，点在线段上.

    （1）若是中点，证明：平面；

    （2）当时，求直线与平面所成角的正弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)讨论函数的单调性；

    (2)若函数存在两个极值点且满足，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=cos（2x-）．

    （1）利用“五点法”，完成以下表格，并画出函数f（x）在一个周期上的图象；

    （2）求函数f（x）的单调递减区间和对称中心的坐标；

    （3）如何由y=cosx的图象变换得到f（x）的图象．

    2x-

    0

    π

    2π

    x

    f（x）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥P-ABCD中，△PBC为正三角形，AB⊥平面PBC，AB∥CD，AB=DC， .

    (1)求证：AE∥平面PBC；

    (2)求证：AE⊥平面PDC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，面积为的正方形中有一个不规则的图形，可按下面方法估计的面积：在正方形中随机投掷个点，若个点中有个点落入中，则的面积的估计值为，假设正方形的边长为2， 的面积为1，并向正方形中随机投掷个点，以表示落入中的点的数目．

    （I）求的均值；

    （II）求用以上方法估计的面积时， 的面积的估计值与实际值之差在区间内的概率．

    附表：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，多面体ABCDEF中，四边形ABCD是矩形，EF∥AD，FA⊥面ABCD，AB=AF=EF=1，AD=2，AC交BD于点P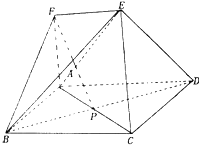

    （1）证明：PF∥面ECD；
    （2）求二面角B﹣EC﹣A的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数y=sin（ωx+ ）向右平移 个单位后，所得的图象与原函数图象关于x轴对称，则ω的最小正值为（ ）
    A.1
    B.2
    C.
    D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《城市规划管理意见》里面提出“新建住宅要推广街区制，原则上不再建设封闭住宅小区，已建成的封闭小区和单位大院要逐步打开”，这个消息在网上一石激起千层浪，各种说法不一而足.某网站为了解居民对“开放小区”认同与否，从岁的人群中随机抽取了人进行问卷调查，并且做出了各个年龄段的频率分布直方图（部分）如图所示，同时对人对这“开放小区”认同情况进行统计得到下表：

    （Ⅰ）完成所给的频率分布直方图，并求的值；

    （Ⅱ）如果从两个年龄段中的“认同”人群中，按分层抽样的方法抽取6人参与座谈会，然后从这6人中随机抽取2人作进一步调查，求这2人的年龄都在内的概率 .

    查看答案和解析>>

    同步练习册答案