
(08年黄冈市模拟理) (12分)在五棱锥P―ABCDE中,PA=AB=AE=2a, PB=PE=2![]() a, BC=DE=a, ∠EAB=∠ABC=∠DEA=90°.
a, BC=DE=a, ∠EAB=∠ABC=∠DEA=90°.
(1)求证:PA![]() 平面ABCDE;
平面ABCDE;
(2)求二面角A―PD―C的大小;
(3)在线段BC上是否存在一点Q,使Q到平面PDE的距离为![]() .
.

解析:(1)由PA⊥AE,PA⊥AB得PA⊥平面ABCD ……4分
(2)过C作CM⊥AD,MN⊥PD于N,连CN,则∠CNM为二面角A―PD―C的一个平面角,……5分
CD=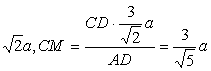 ,
,
![]() ,所求二面角的大小为
,所求二面角的大小为![]() ……8分
……8分
(3)假设存在Q点,过Q作QF∥AB交AE于F,由ED∥AB得QF∥平面PDE,
由DE⊥平面PAE,所以平面PAE⊥平面PED,作FH⊥PE交PE于H,则FH⊥平
面PED,在Rt△EFH中,FH=![]() ,∠FEH=45°,所以FE=
,∠FEH=45°,所以FE=![]() ,所以Q是
,所以Q是
BC中点…………12分
解法二(2)建立如图坐标系,设A(0,0,0),P(0,0,2a),D(a,2a,0),C(2a,a,0),
E(0,2a,0),设平面PAD的法向量为![]() ,
,
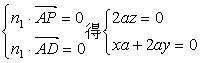 所以
所以![]() ,
,
同理平面PDC的法向量![]() ,
,
![]()
故所求二面角的大小为![]()
(3)![]() ,
,![]() ,可求得平面PDE的法向量
,可求得平面PDE的法向量![]()
设Q(2a,x,0)点Q到平面PED距离为d,![]()
则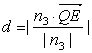 =
=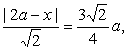 得
得![]() ,由0<x<a得
,由0<x<a得![]()
即Q为BC中点



科目:高中数学 来源: 题型:
(08年黄冈市模拟理) (12分) 在钝角三角形ABC中,AC=2, AB=1, 其面积为![]() ,O是其外心,设
,O是其外心,设![]() ,
,![]() .
.
(1)求![]() ;
;
(2)设![]() s
s![]() +t
+t![]() , 求s、t的值.
, 求s、t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年黄冈市模拟理)(12分)某种彩票在一年内中奖号码的首位数字(如023的0)构成一个分布,数字0,1,2,…,9出现的概率满足![]() =f(x)=a
=f(x)=a![]() (a为常数),现在从这些中奖号码中任取一个,记其首位数字为
(a为常数),现在从这些中奖号码中任取一个,记其首位数字为![]() .
.
(1)求![]() 的分布列;
的分布列;
(2)求![]() 的期望
的期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年黄冈市模拟理) (13分)动圆P与定圆O1:x2+y2+4x-5=0和O2:x2+y2-4x+3=0均外切,设P点的轨迹为C.
(1)求C的方程;
(2)过点A(3,0)作直线![]() 交曲线C于P、Q两点,交y轴于M点,若
交曲线C于P、Q两点,交y轴于M点,若![]() ,当
,当![]() 时,求m的取值范围.
时,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com