
【题目】已知![]() .
.
(1)若![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的值;
的值;
(2)当![]() 时,若
时,若![]() ,都有
,都有![]() 成立,求实数
成立,求实数
![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用![]() 是函数
是函数![]() 的极值点,求出
的极值点,求出![]() ,即可求出
,即可求出![]() 的值;(2)对
的值;(2)对![]() 进行配方,讨论其最值问题,根据题意
进行配方,讨论其最值问题,根据题意![]() ,总有
,总有![]() 成立,只要要求
成立,只要要求![]() ,即可,从而求出
,即可,从而求出![]() 的范围.
的范围.
试题解析:(1)![]() ,又因为
,又因为![]() 是极值点,则
是极值点,则![]() ,则
,则![]() ,经检验,当
,经检验,当![]() 时,
时, ![]() 是
是![]() 极值点,故名满足题意.
极值点,故名满足题意.
(2)当a=2时,f(x)=2x-![]() -5ln x,
-5ln x,
f ′(x)=![]() ,
,
∴当x∈(0, ![]() )时,f ′ (x)>0,f(x)单调递增;
)时,f ′ (x)>0,f(x)单调递增;
当x∈(![]() ,1)时,f ′(x)<0,f(x)单调递减.
,1)时,f ′(x)<0,f(x)单调递减.
∴在(0,1)上,f(x)max=f(![]() )=-3+5ln2.
)=-3+5ln2.
又“x1∈(0,1),x2∈[1,2],都有f(x1)≥g(/span>x2)成立”等价于“f(x)在(0,1)上的最大值不小于g(x)在[1,2]上的最大值”,而g(x)在[1,2]上的最大值为max{g(1),g(2)},
∴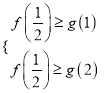 ,即
,即![]() ,
,
解得m≥8-5ln 2.
∴实数m的取值范围是[8-5ln 2,+∞).


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:高中数学 来源: 题型:
【题目】某厂每日生产一种大型产品1件,每件产品的投入成本为2000元.产品质量为一等品的概率为![]() ,二等品的概率为
,二等品的概率为![]() ,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
(1)求在连续生产3天中,恰有一天生产的两件产品都为一等品的的概率;
(2)已知该厂某日生产的2件产品中有一件为一等品,求另一件也为一等品的概率;
(3)求该厂每日生产该种产品所获得的利润![]() (元)的分布列及数学期望.
(元)的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1 , F2是双曲线C: ![]() (a>0,b>0)的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若△ABF2为等边三角形,则双曲线的离心率为( )
(a>0,b>0)的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若△ABF2为等边三角形,则双曲线的离心率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知条件p:x2﹣3x﹣4≤0;条件q:x2﹣6x+9﹣m2≤0,若p是q的充分不必要条件,则m的取值范围是( )
A.[﹣1,1]
B.[﹣4,4]
C.(﹣∞,﹣1]∪[1,+∞)
D.(﹣∞,﹣4]∪[4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x∈R,cos2x﹣sinx+2≤m;q:函数 ![]() 在[1,+∞)上单调递减.
在[1,+∞)上单调递减.
(I)若p∧q为真命题,求m的取值范围;
(II)若p∨q为真命题,p∧q为假命题,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足Sn= ![]() n2+
n2+ ![]() n(n∈N*),数列{bn}是首项为4的正项等比数列,且2b2 , b3﹣3,b2+2成等差数列. (Ⅰ)求数列{an},{bn}的通项公式;
n(n∈N*),数列{bn}是首项为4的正项等比数列,且2b2 , b3﹣3,b2+2成等差数列. (Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)令cn=anbn(n∈N*),求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB= ![]() ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°. 
(1)若PB= ![]() ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业开发一种新产品,现准备投入适当的广告费,对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万件)之间的函数关系为 ![]() ,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为(32Q+3)150%+x50%,而当年产销量相等.
,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为(32Q+3)150%+x50%,而当年产销量相等.
(1)试将年利润P(万件)表示为年广告费x(万元)的函数;
(2)当年广告费投入多少万元时,企业年利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com