
【题目】已知函数f(x)=loga(1+x),g(x)=loga(1-x),(a>0,a≠1).
(1)设a=2,函数f(x)的定义域为[3,63],求f(x)的最值;
(2)求使f(x)-g(x)>0的x的取值范围.
【答案】(1)最小值为2,最大值为6;(2)a>1时,解集为{x|0<x<1},0<a<1时,解集为{x|-1<x<0}.
【解析】试题分析:(1)根据函数单调性求函数最值(2)根据底与1的大小,分类讨论函数单调性,化简不等式,解出x的取值范围.
试题解析:
(1)当a=2时,f(x)=log2(1+x),
在[3,63]上为增函数,因此当x=3时,f(x)最小值为2.
当x=63时f(x)最大值为6.
(2)f(x)-g(x)>0即f(x)>g(x)
当a>1时,loga(1+x)>loga(1-x)
满足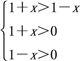 ∴0<x<1
∴0<x<1
当0<a<1时,loga(1+x)>loga(1-x)
满足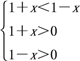 ∴-1<x<0
∴-1<x<0
综上a>1时,解集为{x|0<x<1}
0<a<1时解集为{x|-1<x<0}.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】下列5个命题中正确命题的个数是( )
①对于命题p:x∈R,使得x2+x+1<0,则綈p:x∈R,均有x2+x+1>0;
②m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
③已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则线性回归方程为![]() =1.23x+0.08;
=1.23x+0.08;
④若实数x,y∈[-1,1],则满足x2+y2≥1的概率为![]() ;
;
⑤曲线y=x2与y=x所围成图形的面积是S= (x-x2)dx.
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy上取两个定点![]() 再取两个动点
再取两个动点![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求直线![]() 与
与![]() 交点M的轨迹C的方程;
交点M的轨迹C的方程;
(Ⅱ)过![]() 的直线与轨迹C交于P,Q,过P作
的直线与轨迹C交于P,Q,过P作![]() 轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若
轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(![]() ,简称
,简称![]() )是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为
)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为![]() 等六项.空气质量按照
等六项.空气质量按照![]() 大小分为六级:一级
大小分为六级:一级![]() 为优;二级
为优;二级![]() 为良好;三级
为良好;三级![]() 为轻度污染;四级
为轻度污染;四级![]() 为中度污染;五级
为中度污染;五级![]() 为重度污染;六级
为重度污染;六级![]() 为严重污染.
为严重污染.
某人根据环境监测总站公布的数据记录了某地某月连续10天![]() 的茎叶图如图所示:
的茎叶图如图所示:

(1)利用访样本估计该地本月空气质量优良(![]() )的天数;(按这个月总共30天计算);
)的天数;(按这个月总共30天计算);
(2)若从样本中的空气质量不佳(![]() )的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率.
)的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为![]() ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为![]() 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与![]() ×S成正比,比例系数为
×S成正比,比例系数为![]() ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为![]() ,记
,记![]() 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=![]() 时。
时。
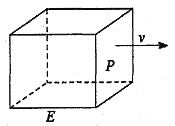
(1)写出![]() 的表达式
的表达式
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度![]() ,使总淋雨量
,使总淋雨量![]() 最少。
最少。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com