
【题目】已知点P(2,-1).
(1)求过P点且与原点距离为2的直线l的方程;
(2)求过P点且与原点距离最大的直线l的方程,最大距离是多少?
【答案】(1)x=2或3x-4y-10=0; (2)![]()
【解析】试题分析:第一步首先考虑直线的斜率不存在的情况,然后可设直线方程的点斜式,根据原点到直线的距离为2,列方程求出斜率,得出直线方程;第二步过P点且与原点距离最大的直线就是过P点与OP垂直的直线,P点与原点距离就是原点到直线距离的最大值,OP长即为所求.
试题解析:
(1)①当l的斜率k不存在时显然满足要求,
∴l的方程为x=2;
②当l的斜率k存在时,设l的方程为y+1=k(x-2),
即kx-y-2k-1=0.
由点到直线距离公式得![]() ,
,
∴k=![]() ,∴l的方程为3x-4y-10=0.
,∴l的方程为3x-4y-10=0.
故所求l的方程为x=2或3x-4y-10=0.
(2)易知过P点与原点O距离最大的直线是过P点且与 PO垂直的直线,由l⊥OP得klkOP=-1,所以![]() =-
=-![]() =2.
=2.
由直线方程的点斜式得y+1=2(x-2),
即2x-y-5=0.
即直线2x-y-5=0是过P点且与原点O距离最大的直线,
最大距离为![]() .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】随着“全面二孩”政策推行,我市将迎来生育高峰.今年新春伊始,宜城各医院产科就已经是一片忙碌,至今热度不减.卫生部门进行调查统计,期间发现各医院的新生儿中,不少都是“二孩”;在市第一医院,共有40个猴宝宝降生,其中20个是“二孩”宝宝;市妇幼保健院共有30个猴宝宝降生,其中10个是“二孩”宝宝. (I)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询.
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(Ⅱ)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
附: ![]()
P(k2>k0) | 0.4 | 0.25 | 0.15 | 0.10 |
k0 | 0.708 | 1.323 | 2.072 | 2.706 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.

(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合.曲线 ![]() (t为参数),曲线C2的极坐标方程为ρ=ρcos2θ+8cosθ. (Ⅰ)将曲线C1 , C2分别化为普通方程、直角坐标方程,并说明表示什么曲线;
(t为参数),曲线C2的极坐标方程为ρ=ρcos2θ+8cosθ. (Ⅰ)将曲线C1 , C2分别化为普通方程、直角坐标方程,并说明表示什么曲线;
(Ⅱ)设F(1,0),曲线C1与曲线C2相交于不同的两点A,B,求|AF|+|BF|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
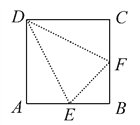
【题目】如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.
问:(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣k(
﹣k( ![]() +lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
+lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
A.(﹣∞,e]
B.[0,e]
C.(﹣∞,e)
D.[0,e)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l1的参数方程为 ![]() ,(t为参数),直线l2的参数方程为
,(t为参数),直线l2的参数方程为  ,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣ ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将三角形ADE沿AE折起,则下列说法正确的是________(填序号).
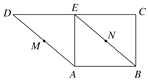
①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置,都有MN⊥AE;③不论D折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com