
【题目】△ABC的内角A,B,C的对边分别为a,b,c,若a=bcosC+csinB.
(1)求B;
(2)求y=sinA-![]() sinC的取值范围.
sinC的取值范围.
【答案】(1)B=![]() ;(2)(-
;(2)(-![]() ,
,![]() ).
).
【解析】
(1)由正弦定理,两角和的正弦函数公式化简已知等式可得cosBsinC=sinCsinB,由sinC≠0,可求cosB=sinB,结合范围0<B<π,可求B的值.
(2)利用三角函数恒等变换的应用,利用余弦函数的图象和性质可求其取值范围.
(1)由正弦定理得:sinA=sinBcosC+sinCsinB,
即sin(B+C)=sinBcosC+sinCsinB,
故cosBsinC=sinCsinB,
因为sinC≠0,
所以cosB=sinB,
因为0<B<π,
所以B=![]() ;
;
(2)因为B=![]() ,
,
所以y=sinA-![]() sinC=sin(
sinC=sin(![]() -C)-
-C)-![]() sinC=sin
sinC=sin![]() cosC-cos
cosC-cos![]() sinC-
sinC-![]() sinC =
sinC =![]() cosC,
cosC,
又因为0<C<![]() ,且y=
,且y=![]() cosC在(0,
cosC在(0,![]() )上单调递减,
)上单调递减,
所以y=sinA-![]() sinC的取值范围是(-
sinC的取值范围是(-![]() ,
,![]() ).
).


科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x与椭圆E:![]() 1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|
1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|![]() .
.

(1)求椭圆E的标准方程;
(2)过点P(1,![]() )的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
)的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,
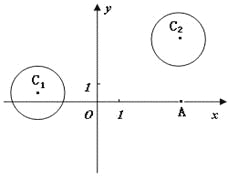
已知圆![]() 和圆
和圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,
,
求直线![]() 的方程;(2)设P为平面上的点,满足:
的方程;(2)设P为平面上的点,满足:
存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,
,
它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]()
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为3的正![]() 的各边三等分,过每个分点分别作另外两边的平行线,称
的各边三等分,过每个分点分别作另外两边的平行线,称![]() 的边及这些平行线所交的10个点为格点.若在这10个格点中任取
的边及这些平行线所交的10个点为格点.若在这10个格点中任取![]() 个格点,一定存在三个格点能构成一个等腰三角形(包括正三角形).求
个格点,一定存在三个格点能构成一个等腰三角形(包括正三角形).求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,随着中国第一款5G手机投入市场,5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析,得到如下规律:每生产手机![]() 万台,其总成本为
万台,其总成本为![]() ,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入
,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入![]() 万元满足
万元满足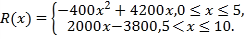
(1)将利润![]() 表示为产量
表示为产量![]() 万台的函数;
万台的函数;
(2)当产量![]() 为何值时,公司所获利润最大?最大利润为多少万元?
为何值时,公司所获利润最大?最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】面对H1N1病毒,各国医疗科研机构都在研究疫苗,现有A、B、C三个独立的研究机构在一定的时期内能研制出疫苗的概率分别是![]() 、
、![]() 、
、![]() .求:
.求:
(1)他们都研制出疫苗的概率;
(2)他们都失败的概率;
(3)只有一个机构研制出疫苗的概率;
(4)至多有一个机构研制出疫苗的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年消毒液和口罩成了抢手年货,老百姓几乎人人都需要,但对于![]() 这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于
这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于![]() 这种口罩了解的占
这种口罩了解的占![]() ,其中45岁以上(含45岁)的人数占
,其中45岁以上(含45岁)的人数占![]() .
.
(1)将答题卡上的列联表补充完整;
(2)判断是否有![]() 的把握认为对
的把握认为对![]() 这种口罩的了解与否与年龄有关.
这种口罩的了解与否与年龄有关.
参考公式: ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com