
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:不详 题型:解答题
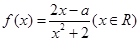
 时,求曲线
时,求曲线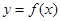 在点
在点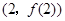 处的切线方程;
处的切线方程;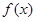 在区间
在区间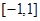 上是增函数,求实数
上是增函数,求实数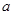 的取值范围
的取值范围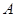 ;
;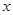 的方程
的方程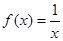 的两个根为
的两个根为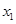 、
、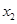 ,若对任意
,若对任意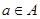 ,
,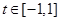 ,不等式
,不等式 恒成立,求
恒成立,求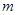 的取值范围.
的取值范围. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
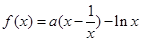
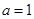 时,求曲线
时,求曲线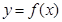 在点
在点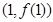 处的切线方程;
处的切线方程;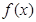 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数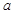 的取值范围;
的取值范围;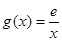 ,若在
,若在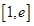 上至少存在一点
上至少存在一点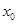 使
使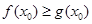 成立,求实数
成立,求实数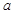 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
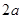 的正方形铁皮的四个角各截去一个边长为
的正方形铁皮的四个角各截去一个边长为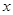 的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度
的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度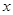 与底面正方形的边长的比不超过常数
与底面正方形的边长的比不超过常数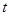 ,问:
,问: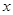 取何值时,长方体的容积V有最大值?
取何值时,长方体的容积V有最大值?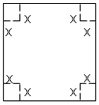
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com