
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的零点个数;
的零点个数;
(2)求证:![]() .
.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)对函数求导,研究函数的单调性,进而得到函数的变化趋势,结合图像得到函数的零点个数;(2)不等式![]() 可化为
可化为![]() ,记
,记![]() ,证得
,证得![]() 即可.
即可.
详解:(1)由题,![]() ,所以当
,所以当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() 有极大值
有极大值![]() .
.
且当![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,所以,当
,所以,当![]() 或
或![]() 时,
时,![]() 恰有一个零点;
恰有一个零点;![]() 时,
时,![]() 有两个零点;
有两个零点;![]() 时,
时,![]() 没有零点.
没有零点.
(2)由(1)可知,![]() .①当
.①当![]() 时,不等式
时,不等式![]() 可化为
可化为![]() ,记
,记![]() ,得
,得![]() .
.
设![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,![]() ,
,![]() 在
在![]() 上图象是不间断的,
上图象是不间断的,
∴存在唯一的实数![]() ,使得
,使得![]() ,∴当
,∴当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上递减,当
上递减,当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上递增,
上递增,
∴当![]() 时,
时,![]() 有极小值,即为最小值,
有极小值,即为最小值,![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() .
.
又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
所以,![]() ,即
,即![]() .
.
②当![]() 时,设
时,设![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,
,
所以![]() ,
,
综上所述,![]() .
.


科目:高中数学 来源: 题型:
【题目】(2018·江西六校联考)在△ABC中,角A,B,C所对的边分别为a,b,c,a=4![]() ,b=4,cosA=-
,b=4,cosA=-![]() .
.
(1)求角B的大小;
(2)若f(x)=cos2x+![]() sin2(x+B),求函数f(x)的单调递增区间.
sin2(x+B),求函数f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在著名的汉诺塔问题中,有三根高度相同的柱子和一些大小及颜色各不相同的圆盘,三根柱子分别为起始柱、辅助柱及目标柱.已知起始柱上套有![]() 个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将
个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将![]() 个圆盘从起始柱移动到目标柱上最少需要移动的次数记为
个圆盘从起始柱移动到目标柱上最少需要移动的次数记为![]() ,则
,则![]() ( )
( )

A. 33B. 31C. 17D. 15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对![]() 表示“甲在
表示“甲在![]() 号车站下车,乙在
号车站下车,乙在![]() 号车站下车”
号车站下车”
(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅲ)求甲、乙两人在不同的车站下车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛的1000同学中,随机抽取60名同学将其成绩(百分制,均为整数)分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)补全频率分布直方图,并估计本次知识竞赛的均分;
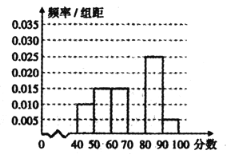
(2)如果确定不低于85分的同学进入复赛,问这1000名参赛同学中估计有多少人进人复赛;
(3)若从第一组,第二组和第六组三组学生中分层抽取6人,再从这6人中随机抽取2人,求所抽取的2人成绩之差的绝对值大于20的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义一:对于一个函数![]() ,若存在两条距离为
,若存在两条距离为![]() 的直线
的直线![]() 和
和![]() ,使得
,使得![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道.
的通道.
定义二:若一个函数![]() 对于任意给定的正数
对于任意给定的正数![]() ,都存在一个实数
,都存在一个实数![]() ,使得函数
,使得函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道,则称
的通道,则称![]() 在正无穷处有永恒通道.
在正无穷处有永恒通道.
下列函数①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() . 其中在正无穷处有永恒通道的函数序号是 .
. 其中在正无穷处有永恒通道的函数序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生物小组为了研究温度对某种酶的活性的影响进行了一组实验,得到的实验数据经整理得到如下的折线图:

(1)由图可以看出,这种酶的活性![]() 与温度
与温度![]() 具有较强的线性相关性,请用相关系数加以说明;
具有较强的线性相关性,请用相关系数加以说明;
(2)求![]() 关于
关于![]() 的线性回归方程,并预测当温度为
的线性回归方程,并预测当温度为![]() 时,这种酶的活性指标值.(计算结果精确到0.01)
时,这种酶的活性指标值.(计算结果精确到0.01)
参考数据:![]() ,
,![]() ,
, ,
,![]() .
.
参考公式:相关系数 .
.
回归直线方程![]() ,
,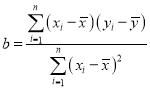 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F是拋物线C:y2=2px(p>0)的焦点,点M(x0,1)在C上,且|MF|=![]() .
.
(1)求p的值;
(2)若直线l经过点Q(3,-1)且与C交于A,B(异于M)两点,证明:直线AM与直线BM的斜率之积为常数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com