
【题目】如图,长方体![]() 的底面
的底面![]() 是正方形,点
是正方形,点![]() 在棱
在棱![]() 上,
上,![]() .
.
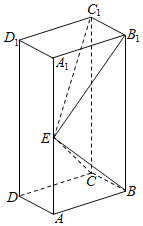
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据长方体性质可知![]() 平面
平面![]() ,从而
,从而![]() ,由题意
,由题意![]() ,即可由线面垂直的判定定理证明
,即可由线面垂直的判定定理证明![]() 平面
平面![]() ;
;
(2)由题意![]() ,设
,设![]() ,建立空间直角坐标系,即可写出各个点的坐标,求得平面
,建立空间直角坐标系,即可写出各个点的坐标,求得平面![]() 和平面
和平面![]() 的法向量,即可由两个平面的法向量求得二面角
的法向量,即可由两个平面的法向量求得二面角![]() 夹角的余弦值,再由同角三角函数关系式即可求得二面角
夹角的余弦值,再由同角三角函数关系式即可求得二面角![]() 的正弦值.
的正弦值.
(1)由已知得,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() .
.
又![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .
.
(2)由(1)知![]() .由题设知
.由题设知![]() ,所以
,所以![]() ,
,
故![]() ,
,![]() . 设
. 设![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 为单位长,建立如图所示的空间直角坐标系
为单位长,建立如图所示的空间直角坐标系![]() :
:
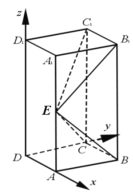
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则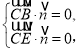 即
即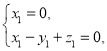 .
.
所以可取![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则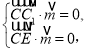 即
即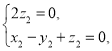
所以可取![]() .
.
于是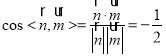 .
.
由同角三角函数关系式可得二面角![]() 的正弦值为
的正弦值为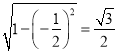 .
.


科目:高中数学 来源: 题型:
【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如表:
月收入(单位百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(Ⅰ)由以上统计数据填下面2×2列联表并问是否有99%的把握认为“月收入以5500为分界点”对“楼市限购令”的态度有差异;
月收入低于55百元的人数 | 月收入不低于55百元的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若采用分层抽样在月收入在[15,25),[25,35)的被调查人中共随机抽取6人进行追踪调查,并给予其中3人“红包”奖励,求收到“红包”奖励的3人中至少有1人收入在[15,25)的概率.
参考公式:K2![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区的“微信健步走”活动情况,现用分层抽样的方法从中抽取老、中、青三个年龄段人员进行问卷调查.已知抽取的样本同时满足以下三个条件:
(i)老年人的人数多于中年人的人数;
(ii)中年人的人数多于青年人的人数;
(iii)青年人的人数的两倍多于老年人的人数.
①若青年人的人数为4,则中年人的人数的最大值为___________.
②抽取的总人数的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,过点
上,过点![]() 作
作![]() 轴于点
轴于点![]()
(1)求线段![]() 的中点的轨迹
的中点的轨迹![]() 的方程
的方程
(2)设![]() 、
、![]() 两点在(1)中轨迹
两点在(1)中轨迹![]() 上,点
上,点![]() ,两直线
,两直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,且(1)中轨迹
,且(1)中轨迹![]() 上存在点
上存在点![]() 满足
满足![]() ,当
,当![]() 面积最小时,求直线
面积最小时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mx-lnx-1(m为常数).
(1)若函数f(x)恰有1个零点,求实数m的取值范围;
(2)若不等式mx-ex≤f(x)+a对正数x恒成立,求实数a的最小整数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com