
分析 由题意和同角三角函数基本关系可得cos(α+β)=$\frac{4}{5}$,cos(β-$\frac{π}{4}$)=-$\frac{5}{13}$,
(1)由诱导公式可得cos(β+$\frac{π}{4}$)=-sin(β-$\frac{π}{4}$)=-$\frac{12}{13}$;
(2)cos(α+$\frac{π}{4}$)=cos[(α+β)-(β-$\frac{π}{4}$)]=cos(α+β)cos(β-$\frac{π}{4}$)+sin(α+β)sin(β-$\frac{π}{4}$),代值计算可得;
(3)由(1)(2)和同角三角函数基本关系可得sin(α+$\frac{π}{4}$)=-$\frac{33}{65}$,sin(β+$\frac{π}{4}$)=-$\frac{5}{13}$,可得cos(α-β)=cos[(α+$\frac{π}{4}$)-(β+$\frac{π}{4}$)]=cos(α+$\frac{π}{4}$)cos(β+$\frac{π}{4}$)+sin(α+$\frac{π}{4}$)sin(β+$\frac{π}{4}$),代值计算可得.
解答 解:∵α,β∈($\frac{3π}{4}$,π),sin(α+β)=-$\frac{3}{5}$,sin(β-$\frac{π}{4}$)=$\frac{12}{13}$,
∴cos(α+β)=$\frac{4}{5}$,cos(β-$\frac{π}{4}$)=-$\frac{5}{13}$,
(1)cos(β+$\frac{π}{4}$)=cos[(β-$\frac{π}{4}$)+$\frac{π}{2}$]=-sin(β-$\frac{π}{4}$)=-$\frac{12}{13}$;
(2)cos(α+$\frac{π}{4}$)=cos[(α+β)-(β-$\frac{π}{4}$)]
=cos(α+β)cos(β-$\frac{π}{4}$)+sin(α+β)sin(β-$\frac{π}{4}$)
=$\frac{4}{5}×(-\frac{5}{13})$+(-$\frac{3}{5}$)×$\frac{12}{13}$=-$\frac{56}{65}$;
(3)结合题意由(1)(2)可得sin(α+$\frac{π}{4}$)=-$\frac{33}{65}$,sin(β+$\frac{π}{4}$)=-$\frac{5}{13}$
∴cos(α-β)=cos[(α+$\frac{π}{4}$)-(β+$\frac{π}{4}$)]
=cos(α+$\frac{π}{4}$)cos(β+$\frac{π}{4}$)+sin(α+$\frac{π}{4}$)sin(β+$\frac{π}{4}$)
=$(-\frac{56}{65})×(-\frac{12}{13})$+$(-\frac{33}{65})×(-\frac{5}{13})$=$\frac{837}{845}$
点评 本题考查两角和与差的三角函数公式,涉及整体法和诱导公式以及同角三角函数基本关系,属中档题.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
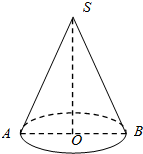 如图,在圆锥SO中,其母线长为2,底面半径为$\frac{1}{2}$,一只虫子从底面圆周上一点A出发沿圆锥表面爬行一周后又回到A点,则这只虫子所爬过的最短路程是2$\sqrt{2}$.
如图,在圆锥SO中,其母线长为2,底面半径为$\frac{1}{2}$,一只虫子从底面圆周上一点A出发沿圆锥表面爬行一周后又回到A点,则这只虫子所爬过的最短路程是2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 施化肥量x | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 水稻产量y | 330 | 345 | 365 | 405 | 445 | 450 | 455 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图的平面直角坐标系中,O为坐标原点,点B在单位圆上,A(2,0),∠AOB=θ,△ABC为等边三角形.
如图的平面直角坐标系中,O为坐标原点,点B在单位圆上,A(2,0),∠AOB=θ,△ABC为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
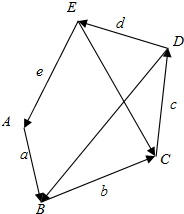 向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{e}$如图所示,解答下列各题:
向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{e}$如图所示,解答下列各题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com