
【题目】在平面直角坐标系xOy中,已知直线l的参数方程为 ![]() (t为参数,0<α<π),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=
(t为参数,0<α<π),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ= ![]() (p>0).
(p>0).
(Ⅰ)写出直线l的极坐标方程和曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C相交于A,B两点,求 ![]() +
+ ![]() 的值.
的值.
【答案】解:(I)由 ![]() 得
得  ,∴直线l的普通方程为
,∴直线l的普通方程为 ![]() ﹣
﹣ ![]() =0,即sinαx﹣cosαy=0. 把x=ρcosθ,y=ρsinθ代入普通方程得sinαρcosθ﹣cosαρsinθ=0.
=0,即sinαx﹣cosαy=0. 把x=ρcosθ,y=ρsinθ代入普通方程得sinαρcosθ﹣cosαρsinθ=0.
∵ρ= ![]() ,∴p=ρ﹣ρcosθ=ρ﹣x,∴ρ=p+x,两边平方得ρ2=x2+2px+p2 , ∴x2+y2=x2+2px+p2 , 即y2﹣2px﹣p2=0.
,∴p=ρ﹣ρcosθ=ρ﹣x,∴ρ=p+x,两边平方得ρ2=x2+2px+p2 , ∴x2+y2=x2+2px+p2 , 即y2﹣2px﹣p2=0.
(II)联立方程组 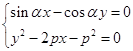 ,解得
,解得 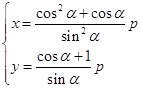 或
或 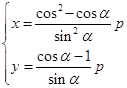 .
.
∴|OA|2=( ![]() )2+(
)2+( ![]() )2=
)2= ![]() ,|OB|2=(
,|OB|2=( ![]() )2+(
)2+( ![]() )2=
)2= ![]() ,
,
∴|OA|= ![]() ,|OB|=
,|OB|= ![]() .
.
∴ ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() (
( ![]() +
+ ![]() )=
)= ![]()
【解析】(1)分别用x,y表示t,消去参数得到普通方程,再化为极坐标方程;(2)联立方程组解出A,B坐标,代入两点间的距离公式得出|OA|,|OB|,再进行化简计算.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥PB,PC=2. 
(1)求证:平面PAB⊥平面ABCD;
(2)若PA=PB,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,AB∥CD,
中,AB∥CD,![]() ,且
,且![]() .现以
.现以![]() 为一边向梯形外作正方形
为一边向梯形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使平面
翻折,使平面![]() 与平面
与平面![]() 垂直,如图2.
垂直,如图2.


(Ⅰ)求证:BC⊥平面DBE;
(Ⅱ)求点D到平面BEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在(0,+∞)上的函数f(x)满足xf′(x)﹣f(x)=xlnx,f( ![]() )=
)= ![]() ,则f(x)( )
,则f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值,又有极小值
D.既无极大值,也无极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合,若曲线C的参数方程为 ![]() (α是参数),直线l的极坐标方程为
(α是参数),直线l的极坐标方程为 ![]() ρsin(θ﹣
ρsin(θ﹣ ![]() )=1.
)=1.
(1)将曲线C的参数方程化为极坐标方程;
(2)由直线l上一点向曲线C引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(x+ ![]() ),x∈R,且f(
),x∈R,且f( ![]() )=
)= ![]() .
.
(1)求A的值;
(2)若f(θ)+f(﹣θ)= ![]() ,θ∈(0,
,θ∈(0, ![]() ),求f(
),求f( ![]() ﹣θ).
﹣θ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com