
【题目】已知函数f(x)在(﹣1,+∞)上单调,且函数y=f(x﹣2)的图象关于x=1对称,若数列{an}是公差不为0的等差数列,且f(a50)=f(a51),则{an}的前100项的和为( )
A.﹣200
B.﹣100
C.0
D.﹣50
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x﹣2)2+(y﹣3)2=1交于点M、N两点.
(1)求k的取值范围;
(2)若 ![]()
![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服务电话,打进的电话响第1声时被接的概率是0.1;响第2声时被接的概率是0.2;响第3声时被接的概率是0.3;响第4声时被接的概率是0.35.
(1)打进的电话在响5声之前被接的概率是多少?
(2)打进的电话响4声而不被接的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班从6名干部中(其中男生4人,女生2人)选3人参加学校的义务劳动.
(1)设所选3人中女生人数为ξ,求ξ的分布列及Eξ;
(2)求男生甲或女生乙被选中的概率;
(3)在男生甲被选中的情况下,求女生乙也被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一支车队有![]() 辆车,某天依次出发执行运输任务。第一辆车于下午
辆车,某天依次出发执行运输任务。第一辆车于下午![]() 时出发,第二辆车于下午
时出发,第二辆车于下午![]() 时
时![]() 分出发,第三辆车于下午
分出发,第三辆车于下午![]() 时
时![]() 分出发,以此类推。假设所有的司机都连续开车,并都在下午
分出发,以此类推。假设所有的司机都连续开车,并都在下午![]() 时停下来休息.
时停下来休息.
到下午![]() 时,最后一辆车行驶了多长时间?
时,最后一辆车行驶了多长时间?
如果每辆车的行驶速度都是![]() ,这个车队当天一共行驶了多少
,这个车队当天一共行驶了多少![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值m | m<185 | 185≤m<205 | m≥205 |
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图: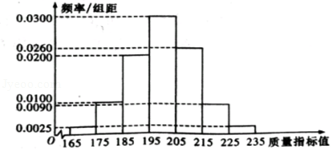
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(Ⅱ)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(III)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(218,140}),则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com