
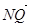 = 2
= 2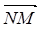 .
.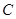 的方程;
的方程;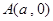 ,点
,点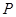 为曲线
为曲线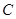 上任一点,求点
上任一点,求点 到点
到点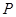 距离的最大值
距离的最大值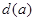 ;
;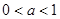 的条件下,设△
的条件下,设△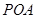 的面积为
的面积为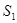 (
(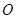 是坐标原点,
是坐标原点,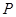 是曲线
是曲线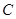 上横坐标为
上横坐标为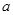 的点),以
的点),以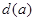 为边长的正方形的面积为
为边长的正方形的面积为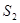 .若正数
.若正数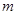 满足
满足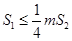 ,问
,问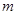 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
 时,
时,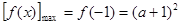 ;
; 时,
时, ;
; 时,,
时,, .所以,
.所以,

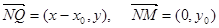
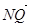 =
=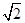
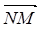
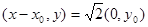
 ∴
∴

 .........................4分
.........................4分 ,则
,则
 ,令
,令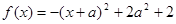 ,
, ,所以,
,所以, ,即
,即 时
时 在
在 上是减函数,
上是减函数,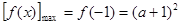 ;
;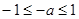 ,即
,即 时,
时, 在
在 上是增函数,在
上是增函数,在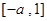 上是减函数,则
上是减函数,则 ;
; ,即
,即 时,
时, 在
在 上是增函数,
上是增函数, .
. . 9分
. 9分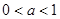 时,
时, ,于是
,于是 ,
, ,
,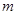 满足条件,则
满足条件,则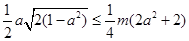 ,即
,即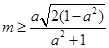 ,
,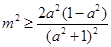 ,令
,令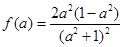 ,设
,设 ,则
,则 ,
,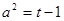 ,于是
,于是 ,
, ,即
,即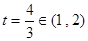 时,
时, ,
, ,
, .所以,
.所以,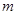 存在最小值
存在最小值 . 14分
. 14分

 金钥匙试卷系列答案
金钥匙试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com