
【题目】下列说法错误的是( )
A.回归直线过样本点的中心![]() .
.
B.对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小
C.两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1
D.在回归直线方程![]() =0.2x+0.8中,当解释变量x每增加1个单位时,预报变量
=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量![]() 平均增加0.2个单位
平均增加0.2个单位
科目:高中数学 来源: 题型:
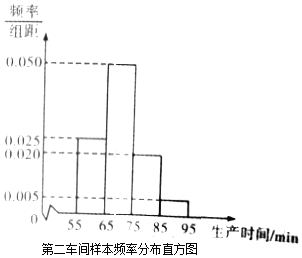
【题目】某工厂有两个车间生产同一种产品,第一车间有工人200人,第二车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,并对他们中每位工人生产完成一件产品的时间(单位:min)分别进行统计,得到下列统计图表(按照[55,65),[65,75),[75,85),[85,95]分组).
分组 | 频数 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合计 | 20 |
第一车间样本频数分布表
(Ⅰ)分别估计两个车间工人中,生产一件产品时间小于75min的人数;
(Ⅱ)分别估计两车间工人生产时间的平均值,并推测哪个车间工人的生产效率更高?(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)从第一车间被统计的生产时间小于75min的工人中,随机抽取3人,记抽取的生产时间小于65min的工人人数为随机变量X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】边长为![]() 的等边三角形内任一点到三边距离之和为定值,这个定值等于
的等边三角形内任一点到三边距离之和为定值,这个定值等于![]() ;将这个结论推广到空间是:棱长为
;将这个结论推广到空间是:棱长为![]() 的正四面体内任一点到各面距离之和等于________________.(具体数值)
的正四面体内任一点到各面距离之和等于________________.(具体数值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在![]() 年的自主招生考试成绩中随机抽取
年的自主招生考试成绩中随机抽取![]() 名学生的笔试成绩,按成绩分组:第
名学生的笔试成绩,按成绩分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() 得到的频率分布直方图如图所示
得到的频率分布直方图如图所示
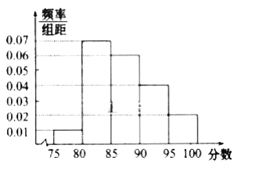
![]() 分别求第
分别求第![]() 组的频率;
组的频率;
![]() 若该校决定在第
若该校决定在第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名学生进入第二轮面试,
名学生进入第二轮面试,
![]() 已知学生甲和学生乙的成绩均在第
已知学生甲和学生乙的成绩均在第![]() 组,求学生甲和学生乙同时进入第二轮面试的概率;
组,求学生甲和学生乙同时进入第二轮面试的概率;
![]() 根据直方图试估计这
根据直方图试估计这![]() 名学生成绩的平均分.(同一组中的数据用改组区间的中间值代表)
名学生成绩的平均分.(同一组中的数据用改组区间的中间值代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
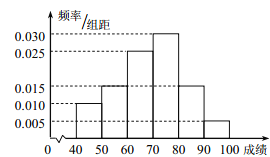
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
(1)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
附表及公式:
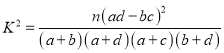 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学进入新华书店购买数学课外阅读书籍,经过筛选后,他们都对![]() 三种书籍有购买意向,已知甲同学购买书籍
三种书籍有购买意向,已知甲同学购买书籍![]() 的概率分别为
的概率分别为![]() ,乙同学购买书籍
,乙同学购买书籍![]() 的概率分别为
的概率分别为![]() ,假设甲、乙是否购买
,假设甲、乙是否购买![]() 三种书籍相互独立.
三种书籍相互独立.
(1)求甲同学购买3种书籍的概率;
(2)设甲、乙同学购买2种书籍的人数为![]() ,求
,求![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com