
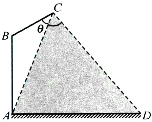
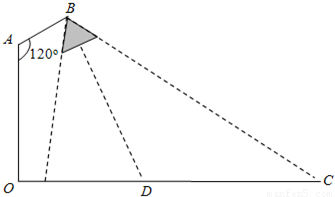
 在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与道路垂直,且∠ABC=120°,路灯C采用锥形灯罩,射出的光线如图中阴影部分所示,已知∠ACD=60°,路宽AD=24m.设灯柱高AB=h(m),∠ACB=θ(30°≤θ≤45°).
在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与道路垂直,且∠ABC=120°,路灯C采用锥形灯罩,射出的光线如图中阴影部分所示,已知∠ACD=60°,路宽AD=24m.设灯柱高AB=h(m),∠ACB=θ(30°≤θ≤45°).| 3 |
 解:(1)如图所示:由于∠ABC=120°,∠ACB=θ,∴∠BAC=60°-θ.
解:(1)如图所示:由于∠ABC=120°,∠ACB=θ,∴∠BAC=60°-θ.| AC |
| sin∠ADC |
| AD |
| sin∠ACD |
| AC |
| sin(90°-θ) |
| 24 |
| sin60° |
| 3 |
| AB |
| sin∠ACB |
| AC |
| sin∠ABC |
| h |
| sinθ |
16
| ||
| sin120° |
| BC |
| sin∠BAC |
| AC |
| sin∠ABC |
| BC |
| sin(60°-θ) |
16
| ||
| sin120° |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
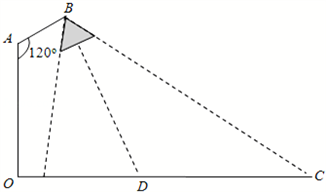
 在路边安装路灯,灯柱OA的高为h,路宽OC为23米,灯杆AB的长为2.5米,且与灯柱OA成120°角.路灯采用锥形灯罩,灯罩轴线BD与灯杆AB垂直.请你建立适当的直角坐标系,解决以下问题:
在路边安装路灯,灯柱OA的高为h,路宽OC为23米,灯杆AB的长为2.5米,且与灯柱OA成120°角.路灯采用锥形灯罩,灯罩轴线BD与灯杆AB垂直.请你建立适当的直角坐标系,解决以下问题:查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省高三5月高考模拟考试理科数学试卷(解析版) 题型:解答题
如图,在路边安装路灯,灯柱与地面垂直,灯杆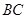 与灯柱
与灯柱 所在平面与道路垂直,且
所在平面与道路垂直,且 ,路灯
,路灯 采用锥形灯罩,射出的光线如图阴影部分所示,已知
采用锥形灯罩,射出的光线如图阴影部分所示,已知 ,路宽
,路宽 ,设灯柱高
,设灯柱高 ,
, .
.

(1)求灯柱的高 (用
(用 表示);
表示);
(2)若灯杆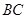 与灯柱
与灯柱 所用材料相同,记所用材料长度和为
所用材料相同,记所用材料长度和为 ,求
,求 关于
关于 的函数表达式,并求出
的函数表达式,并求出 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:江苏期中题 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省无锡市江阴二中高二(上)期中数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com