
 ,结果保留三位有效数字)
,结果保留三位有效数字)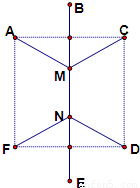
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 某大学为了发展需要,准备兴建新校区.新校区规划分南北两个校区,北区拟建A,B,C三个不同功能的教学小区,南区拟建D,E,F三个不同功能的生活小区.南北校区用一条中心主干道MN相连,各功能小区与中心主干道用支道相连,并且各功能小区到中心干道的端点的距离相等,A,C,D,F在边长为2公里的正方形顶点位置,B,E分别在MN的延长线上.已知中心主干道的造价为每公里30万元,支道造价为每公里20万元.问当中心主干道约为多少公里时,才能使道路总造价最低?道路总造价最低为多少万元?( 参考数据
某大学为了发展需要,准备兴建新校区.新校区规划分南北两个校区,北区拟建A,B,C三个不同功能的教学小区,南区拟建D,E,F三个不同功能的生活小区.南北校区用一条中心主干道MN相连,各功能小区与中心主干道用支道相连,并且各功能小区到中心干道的端点的距离相等,A,C,D,F在边长为2公里的正方形顶点位置,B,E分别在MN的延长线上.已知中心主干道的造价为每公里30万元,支道造价为每公里20万元.问当中心主干道约为多少公里时,才能使道路总造价最低?道路总造价最低为多少万元?( 参考数据| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com