
【题目】已知函数![]() 的两个极值点为
的两个极值点为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 在
在![]() (其中
(其中![]() 上是单调函数, 求
上是单调函数, 求![]() 的取值范围;
的取值范围;
(3)当![]() 时, 求证:
时, 求证:![]() .
.
【答案】(1)![]() (2)
(2)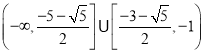 (3)详见解析
(3)详见解析
【解析】
试题分析:(1)由极值定义得![]() 得两根为
得两根为![]() ,由韦达定理得
,由韦达定理得![]() ,解得
,解得![]() ,再根据二次方程求根公式得
,再根据二次方程求根公式得![]() (2)由(1)可得函数有三个单调区间,由于
(2)由(1)可得函数有三个单调区间,由于![]() ,所以
,所以![]() 为单调区间的一个子集,即
为单调区间的一个子集,即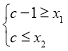 或
或![]() ,(3)利用不等式乘积性质证明不等式:利用导数可得
,(3)利用不等式乘积性质证明不等式:利用导数可得![]() 先将后增,有最小值
先将后增,有最小值![]() 所以
所以![]() ;根据二次函数最值得
;根据二次函数最值得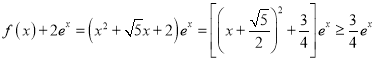 ,由于两个不等式中等号取法不一致,所以乘积中等号取不到
,由于两个不等式中等号取法不一致,所以乘积中等号取不到
试题解析:(1)![]() 由
由![]()
得![]() ,
,
![]() 由
由![]() 得
得![]() .
.
(2)由(1)知,![]() 在
在![]() 上递减, 在
上递减, 在![]() 上递增, 其中
上递增, 其中![]() ,
,
当![]() 在
在![]() 上递减时,
上递减时,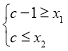 , 又
, 又![]() ,当
,当![]() 在
在![]() 上递增时,
上递增时,![]() , 综上,
, 综上, ![]() 的取值范围为
的取值范围为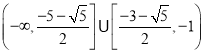 .
.
(3)证明: 设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.![]() ,
,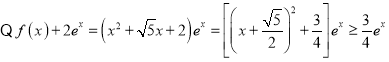 (当
(当![]() 时取等号),
时取等号),
![]() 不等式成立(因为取等条件不相同, 所以等号取不到).
不等式成立(因为取等条件不相同, 所以等号取不到).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知数据![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为
是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上马云2016年10月份的收入
,如果再加上马云2016年10月份的收入![]() (约100亿元),则相对于
(约100亿元),则相对于![]() 、
、![]() 、
、![]() ,这101个月收入数据( )
,这101个月收入数据( )
A.平均数可能不变,中位数可能不变,方差可能不变
B.平均数大大增大,中位数可能不变,方差也不变
C.平均数大大增大,中位数一定变大,方差可能不变
D.平均数大大增大,中位数可能不变,方差变大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节期间某超市搞促销活动,当顾客购买商品的金额达到一定数量后可以参加抽奖活动,活动规则为:从装有![]() 个黑球,
个黑球, ![]() 个红球,
个红球, ![]() 个白球的箱子中(除颜色外,球完全相同)摸球.
个白球的箱子中(除颜色外,球完全相同)摸球.
(Ⅰ)当顾客购买金额超过![]() 元而不超过
元而不超过![]() 元时,可从箱子中一次性摸出
元时,可从箱子中一次性摸出![]() 个小球,每摸出一个黑球奖励
个小球,每摸出一个黑球奖励![]() 元的现金,每摸出一个红球奖励
元的现金,每摸出一个红球奖励![]() 元的现金,每摸出一个白球奖励
元的现金,每摸出一个白球奖励![]() 元的现金,求奖金数不少于
元的现金,求奖金数不少于![]() 元的概率;
元的概率;
(Ⅱ)当购买金额超过![]() 元时,可从箱子中摸两次,每次摸出
元时,可从箱子中摸两次,每次摸出![]() 个小球后,放回再摸一次,每摸出一个黑球和白球一样奖励
个小球后,放回再摸一次,每摸出一个黑球和白球一样奖励![]() 元的现金,每摸出一个红球奖励
元的现金,每摸出一个红球奖励![]() 元的现金,求奖金数小于
元的现金,求奖金数小于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央电视台电视公开课《开讲了》需要现场观众,先邀请甲、乙、丙、丁四所大学的40名学生参加,各大学邀请的学生如下表所示:
大学 | 甲 | 乙 | 丙 | 丁 |
人数 | 8 | 12 | 8 | 12 |
从这40名学生中按分层抽样的方式抽取10名学生在第一排发言席就座.
(1)求各大学抽取的人数;
(2)从(1)中抽取的乙大学和丁大学的学生中随机选出2名学生发言,求这2名学生来自同一所大学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,若存在闭区间[m,n]
,若存在闭区间[m,n] ![]() D,使得函数
D,使得函数![]() 满足:①
满足:①![]() 在[m,n]上是单调函数;②
在[m,n]上是单调函数;②![]() 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为![]() 的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA![]() =4,点D是AB的中点
=4,点D是AB的中点

(1)求证:AC![]() BC
BC![]() ;
;
(2)求证:AC![]() //平面CDB
//平面CDB![]() ;
;
(3)求二面角B-DC-B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某公司技术升级后生产![]() 产品过程中记录的产量
产品过程中记录的产量![]() (吨)与相应的成本
(吨)与相应的成本![]() (万元)的几组对照数据:
(万元)的几组对照数据:

(1)请画出上表数据的散点图;

(2)请根据上表提供的数据,用最小二乘法求出![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(3)已知该公司技术升级前生产100吨![]() 产品的成本为90万元.试根据(2)求出的回归直线方程,预测技术升级后生产100吨
产品的成本为90万元.试根据(2)求出的回归直线方程,预测技术升级后生产100吨![]() 产品的成本比技术升级前约降低多少万元?
产品的成本比技术升级前约降低多少万元?
(附:  ,
, ![]() ,其中
,其中![]() 为样本平均值)
为样本平均值)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com