
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,梯形
中,梯形![]() 与平行四边形
与平行四边形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
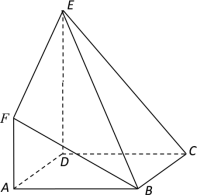
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判断线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求 出
?若存在,求 出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某水文观测点的历史统计数据,得到某河流水位![]() (单位:米)的频率分布直方图如下.将河流水位在
(单位:米)的频率分布直方图如下.将河流水位在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 各段内的频率作为相应段的概率,并假设每年河流水位变化互不影响.
各段内的频率作为相应段的概率,并假设每年河流水位变化互不影响.
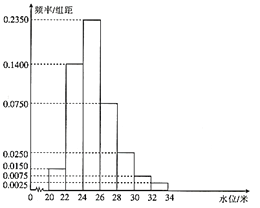
(1)求未来4年中,至少有2年该河流水位![]() 的概率(结果用分数表示).
的概率(结果用分数表示).
(2)已知该河流对沿河![]() 工厂的影响如下:当
工厂的影响如下:当![]() 时,不会造成影响;当
时,不会造成影响;当![]() 时,损失50000元;当
时,损失50000元;当![]() 时,损失300000元.为减少损失,
时,损失300000元.为减少损失,![]() 工厂制定了三种应对方案.
工厂制定了三种应对方案.
方案一:不采取措施;
方案二:防御不超过30米的水位,需要工程费用8000元;
方案三:防御34米的最高水位,需要工程费用20000元.
试问哪种方案更好,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,点E是棱
中,点E是棱![]() 的中点,点F是线段
的中点,点F是线段![]() 上的一个动点.有以下三个命题:
上的一个动点.有以下三个命题:
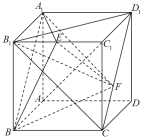
①异面直线![]() 与
与![]() 所成的角是定值;
所成的角是定值;
②三棱锥![]() 的体积是定值;
的体积是定值;
③直线![]() 与平面
与平面![]() 所成的角是定值.
所成的角是定值.
其中真命题的个数是( )
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)求函数![]() 的对称轴方程;
的对称轴方程;
(II)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() 分别是△ABC三个内角A,B,C的对边,a=2,c=4,且
分别是△ABC三个内角A,B,C的对边,a=2,c=4,且![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
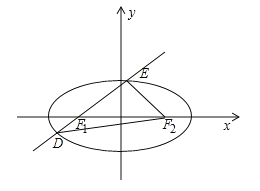
【题目】如图,已知椭圆![]() ,
,![]() 分别为其左、右焦点,过
分别为其左、右焦点,过![]() 的直线与此椭圆相交于
的直线与此椭圆相交于![]() 两点,且
两点,且![]() 的周长为8,椭圆
的周长为8,椭圆![]() 的离心率为
的离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在平面直角坐标系![]() 中,已知点
中,已知点![]() 与点
与点![]() ,过
,过![]() 的动直线
的动直线![]() (不与
(不与![]() 轴平行)与椭圆相交于
轴平行)与椭圆相交于![]() 两点,点
两点,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点.求证:
轴的对称点.求证:
(i)![]() 三点共线.
三点共线.
(ii)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
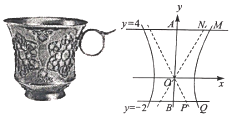
【题目】如图为陕西博物馆收藏的国宝——唐·金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇美,巧夺天工,是唐代金银细作的典范之作.该杯型几何体的主体部分可近似看作是双曲线![]() 的右支与直线
的右支与直线![]() ,
,![]() ,
,![]() 围成的曲边四边形
围成的曲边四边形![]() 绕
绕![]() 轴旋转一周得到的几何体,如图
轴旋转一周得到的几何体,如图![]() 分别为
分别为![]() 的渐近线与
的渐近线与![]() ,
,![]() 的交点,曲边五边形
的交点,曲边五边形![]() 绕
绕![]() 轴旋转一周得到的几何体的体积可由祖恒原理(祖恒原理:幂势既同,则积不容异).意思是:两等高的几何体在同高处被截得的两截面面积均相等,那么这两个几何体的体积相等,那么这两个几何体的体积相等),据此求得该金杯的容积是_____.(杯壁厚度忽略不计)
轴旋转一周得到的几何体的体积可由祖恒原理(祖恒原理:幂势既同,则积不容异).意思是:两等高的几何体在同高处被截得的两截面面积均相等,那么这两个几何体的体积相等,那么这两个几何体的体积相等),据此求得该金杯的容积是_____.(杯壁厚度忽略不计)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com