
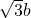 =0.
=0. sinB+sin(C-
sinB+sin(C- )的值域.
)的值域.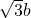 =0
=0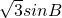 =0,
=0, =0,即sinA=
=0,即sinA= …(5分)
…(5分) 或A=
或A= …(7分)
…(7分)
 …(9分)
…(9分) sinB+sin(C-
sinB+sin(C- )=
)= sinB+sin(
sinB+sin( -B)
-B) sinB+cosB=2sin(B+
sinB+cosB=2sin(B+ ) …(12分)
) …(12分) ),得B+
),得B+ ∈(
∈( ,
, )
) )∈
)∈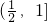 ,可得2sin(B+
,可得2sin(B+ )∈(1,2]
)∈(1,2] sinB+sin(C-
sinB+sin(C- )的值域域为(1,2]…(14分)
)的值域域为(1,2]…(14分)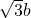 =0得2sinAsinB-
=0得2sinAsinB-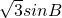 =0,结合sinB>0算出sinA=
=0,结合sinB>0算出sinA= ,由A∈(0,π)即可得到A=
,由A∈(0,π)即可得到A= 或A=
或A= ;
; ,从而得到B+C=
,从而得到B+C= ,将函数y=
,将函数y= sinB+sin(C-
sinB+sin(C- )化简为y=
)化简为y= sinB+sin(
sinB+sin( -B),再由两角差的正弦公式和辅助角公式化简整理,得y=2sin(B+
-B),再由两角差的正弦公式和辅助角公式化简整理,得y=2sin(B+ ),最后根据三角函数的图象与性质,结合角B的取值范围,即可求出函数y=
),最后根据三角函数的图象与性质,结合角B的取值范围,即可求出函数y= sinB+sin(C-
sinB+sin(C- )的值域.
)的值域.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
| π |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com