
【题目】已知函数![]() ,
,![]() .
.
(1)设函数![]() ,若
,若![]() ,求
,求![]() 的极值;
的极值;
(2)设函数![]() ,若
,若![]() 的图象与
的图象与![]() 的图象有
的图象有![]() ,
,![]() 两个不同的交点,证明:
两个不同的交点,证明:![]() .
.
【答案】(1)极大值为![]() ,极小值为
,极小值为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)先求函数![]() 的导函数,再利用导数判断函数的单调性,然后求极值即可;
的导函数,再利用导数判断函数的单调性,然后求极值即可;
(2)函数![]() 的图象与
的图象与![]() 的图象有两个不同的交点,等价于关于
的图象有两个不同的交点,等价于关于![]() 的方程
的方程![]() ,即
,即![]() 有两个不同的根,再构造函数
有两个不同的根,再构造函数![]()
解:(1)因为![]() ,
,
所以![]() ,
,
![]() .
.
令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() ,
,![]() 上单调递增;
上单调递增;
令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
故![]() 的极大值为
的极大值为![]() ,
,
故![]() 的极小值为
的极小值为![]() .
.
(2)证明:![]() ,
,
因为函数![]() 的图象与
的图象与![]() 的图象有两个不同的交点,
的图象有两个不同的交点,
所以关于![]() 的方程
的方程![]() ,即
,即![]() 有两个不同的根.
有两个不同的根.
由题知![]() ①,
①,![]() ②,
②,
①+②得![]() ③,
③,
②-①得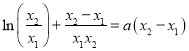 ④.
④.
由③,④得![]() ,
,
不妨设![]() ,记
,记![]() .
.
令![]() ,则
,则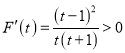 ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
则![]() ,即
,即![]() ,
,
所以![]() .
.
因为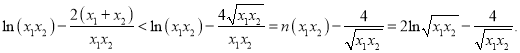
所以![]() ,
,
即![]() .
.
令![]() ,
,
则![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
,
所以![]() ,
,
即![]() ,
,
所以![]() .
.
两边同时取对数可得![]() ,
,
得证.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷(Dirichlet,1805~1859)在数学领域成就显著.19世纪,狄利克雷定义了一个“奇怪的函数” 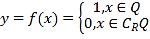 其中R为实数集,Q为有理数集.则关于函数
其中R为实数集,Q为有理数集.则关于函数![]() 有如下四个命题,正确的为( )
有如下四个命题,正确的为( )
A.函数![]() 是偶函数
是偶函数
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一个不为零的有理数T,![]() 对任意的
对任意的![]() 恒成立
恒成立
D.不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“回文数”是指从左到右与从右到左读都一样的正整数,如22,121,3553等.显然2位“回文数”共9个:11,22,33,…,99.现从9个不同2位“回文数”中任取1个乘以4,其结果记为X;从9个不同2位“回文数”中任取2个相加,其结果记为Y.
(1)求X为“回文数”的概率;
(2)设随机变量![]() 表示X,Y两数中“回文数”的个数,求
表示X,Y两数中“回文数”的个数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王想在某市一住宅小区买套新房,据了解,该小区有若干栋互相平行的平顶楼房,每栋楼房有15层,每层楼高为3米,顶楼有1米高的隔热层,两楼之间相距60米.小王不想买最前面和最后面的楼房,但希望所买楼层全年每天正午都能晒到太阳.为此,小王查找了有关地理资料,获得如下一些信息:①该市的纬度(地面一点所在球半径与赤道平面所成的角)为北纬![]() ;②正午的太阳直射北回归线(太阳光线与赤道平面所成的角为
;②正午的太阳直射北回归线(太阳光线与赤道平面所成的角为![]() )时,物体的影子最短,直射南回归线(太阳光线与赤道平面所成的角为
)时,物体的影子最短,直射南回归线(太阳光线与赤道平面所成的角为![]() )时,物体的影子最长,那么小王买房的最低楼层应为( )
)时,物体的影子最长,那么小王买房的最低楼层应为( )
A.3B.4C.5D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com