分析:(Ⅰ)根据
•=0判断出
⊥可知△AF
1F
2为直角三角形,进而可知
||cos∠F1AF2=||进而根据
9•=2.求得
||=3||,进而根据椭圆的定义联立求得
||和| |根据勾股定理建立等式求得a,则椭圆的方程可得.
(Ⅱ)根据题意通过E坐标求出F坐标,代入椭圆的方程,化简
•的表达式,利用P是椭圆上的任意一点纵坐标的范围求出表达式的最大值.
解答:解:(Ⅰ)因为
•=0,所以有
⊥所以△AF
1F
2为直角三角形;
∴
||cos∠F1AF2=||则有
9•=9||||cos∠F1AF2=9||2=2=||2所以,
||=3||又
||+||=2a,
∴
||=,||=在△AF
1F
2中有
||2=||2+||2即
()2=()2+4(a2-1),解得a
2=2
所求椭圆M方程为
+y2=1(Ⅱ)由题意可知N(0,2),E,F关于点N对称,
设E(x
0,y
0),则F(-x
0,4-y
0)有
x02+(y0-2)2=1,
∴
•=x
2-x
02+4y
0-4y-y
02+y
2=x
2+2y
2-(x
02+(y
0-2)
2)-y
2+4-4y=-(y+2)
2+9
P是椭圆M上的任一点,y∈[-1,1],
所以当y=-1时,
•的最大值为8.
点评:本题主要考查了直线与圆锥曲线的问题,向量的基本计算.考查了学生分析问题和解决问题的能力.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案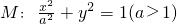 上,直线AB、AC分别过椭圆的左右焦点F1、F2,当
上,直线AB、AC分别过椭圆的左右焦点F1、F2,当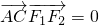 时,有
时,有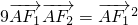 .
. 的最大值.
的最大值.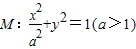 上,直线AB、AC分别过椭圆的左右焦点F1、F2,当
上,直线AB、AC分别过椭圆的左右焦点F1、F2,当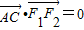 时,有
时,有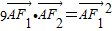 .
.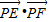 的最大值.
的最大值.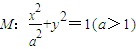 上,直线AB、AC分别过椭圆的左右焦点F1、F2,当
上,直线AB、AC分别过椭圆的左右焦点F1、F2,当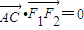 时,有
时,有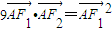 .
.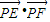 的最大值.
的最大值.