
����Ŀ��2016��3��9����15�գ��ȸ��˹�����ϵͳ����������ӭսΧ��ھ�����ʯ�����ս���������������ܱȷ�4��1սʤ����ʯ����������Ϊ�ⳡ�����������ʤ����Ҳ�������˳ַ��������������Ϊ�˽����˵��飬�ڲμӵ����2548����������1560���ַ��������2452��Ů������1200���ַ����������������Щ����˵�����Ա𡱶��жϡ��˻���ս�������ʤ�����Ƿ��й�ϵʱ��Ӧ���õ�ͳ�Ʒ����ǣ� ��
A.��Ҷͼ
B.�ֲ����
C.�����Լ���
D.�ع�ֱ�߷���
 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪������ԭ�㣬������x���ϵ�˫����C��������Ϊ ![]() ����˫����C��б��Ϊ2��ֱ��l��һ��������P����2��0����
����˫����C��б��Ϊ2��ֱ��l��һ��������P����2��0����
��1����˫����C�ķ��̼����Ľ����߷��̣�
��2������ֱ��l��������Ľ���Ϊ����������ߵı����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��������![]() ʱ������
ʱ������![]() �ĵ������䣻
�ĵ������䣻
��������![]() ��
��![]() ʱ��֤����
ʱ��֤����![]() ������
������![]() Ϊ��Ȼ�����ĵ�����.
Ϊ��Ȼ�����ĵ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
(1)����![]() �ĵ������䣻
�ĵ������䣻
(2)������![]() ���������
���������![]() ��(
��(![]() )����֤��
)����֤�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����һ��뾶��Ϊ1���İ�Բ�θְ壬��Ҫ���н�ȡһ���ڽӵ��� ���β���ABCD�������β���ABCD�����Ϊ![]() ƽ���ף�
ƽ���ף�
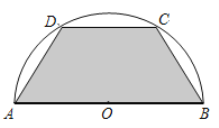
��1��������Ҫ��д��������ϵʽ��
����![]() ����������
����������![]() ��ʾ��
��ʾ��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
����![]() ����
����![]() ��ʾ��
��ʾ��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�������β���ABCD���![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() sin2x��cos2x��
sin2x��cos2x��
��1������f��x������С�����ں����ֵ��
��2������f��x���ĵ����ݼ����䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���A,B,C���Եı߷ֱ���a,b,c,��![]() .
.
������֤����![]() ��
��
��������![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=loga��x+2����1��a��0��a��1����ͼ��������A������A��ֱ��mx+ny+1=0�ϣ�����m��0��n��0���� ![]() +
+ ![]() ����СֵΪ�� ��
����СֵΪ�� ��
A.3+2 ![]()
B.3+2 ![]()
C.7
D.11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() �������ύ��
�������ύ��![]() ����ͼ��.
����ͼ��.
��1����![]() ��Բ
��Բ![]() �ϳ�
�ϳ�![]() �������㣨��ͼ1����
�������㣨��ͼ1����![]() ��ֱ��
��ֱ��![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ����
����![]() ����Сֵ��
����Сֵ��
��2����![]() ��Բ
��Բ![]() �ϳ�
�ϳ�![]() �������㣨��ͼ2����ֱ��
�������㣨��ͼ2����ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() .��
.��![]() ��б��Ϊ
��б��Ϊ![]() ��б��Ϊ
��б��Ϊ![]() ����֤��
����֤�� ![]() Ϊ��ֵ.
Ϊ��ֵ.
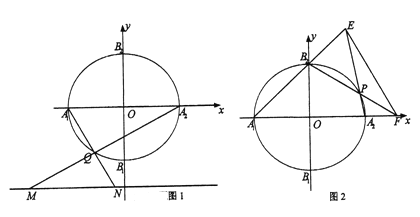
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com