
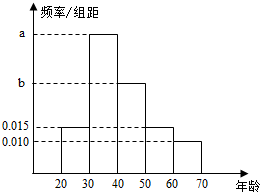
 ����ij��������ƽ̨�ĵ���ͳ����ʾ����������1000λ���������ߵ����������ͼ��ʾ��
����ij��������ƽ̨�ĵ���ͳ����ʾ����������1000λ���������ߵ����������ͼ��ʾ������ ��1��ֱ��ͼ�У�Ƶ��=���������꼰Ƶ�ʺ�Ϊ1���г������飻
��2�������оٷ������еij�ȡ������ô�����ܺ�Ϊ200Ԫ������г������ùŵ�����ʹ�ʽ�����
��� �⣺��1������֪�ɵã�
$\left\{\begin{array}{l}��0.015+a+b+0.015+0.10����10=1\\ 2b=a+0.015\end{array}\right.$��
��ã�a=0.035��b=0.025��
��2�����÷ֲ�����������г�ȡ5�ˣ��������ڸ�������Ⱥ��Ϊ3�ˣ�����DZ��������Ⱥ��Ϊ2�ˣ�
������ѵ���ΪA��B��C��DZ�����ѵ���Ϊa��b������ȡ�����ˣ�
�ܹ��У�ABC��ABa��ABb��ACa��ACb��BCa��BCb��Aab��Bab��Cab��10�������
����ABa��ABb��ACa��ACb��BCa��BCbΪ��ô�����ܺ�Ϊ200Ԫ�������
��ˣ����˻�ô���ȯ�ܺ�Ϊ200Ԫ�ĸ���Ϊ$\frac{3}{5}$��
���� ��С����Ҫ����ͳ������ʵ����֪ʶ��������Ҫ�������ݴ����������ѶȲ������ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
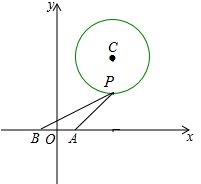 ��ͼ����ƽ��ֱ������ϵ�ڣ���֪A��1��0����B��-1��0�����㣬��ԲC�ķ���Ϊx2+y2-6x-8y+21=0����PΪԲC�ϵĶ��㣮
��ͼ����ƽ��ֱ������ϵ�ڣ���֪A��1��0����B��-1��0�����㣬��ԲC�ķ���Ϊx2+y2-6x-8y+21=0����PΪԲC�ϵĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 0 | C�� | -1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�������������㷨�У���ִ��ѭ����Ĵ���Ϊ1000����ԭ����������ʵ��a��ȡֵ��Χ��1000��a��1001��
��ͼ�������������㷨�У���ִ��ѭ����Ĵ���Ϊ1000����ԭ����������ʵ��a��ȡֵ��Χ��1000��a��1001���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-1��0��1} | B�� | {0��1} | C�� | {0} | D�� | {-1��0} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 22 | B�� | 24 | C�� | 26 | D�� | 28 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4$\sqrt{2}$ | B�� | 2$\sqrt{2}$ | C�� | 2$\sqrt{10}$ | D�� | $\sqrt{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
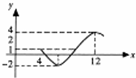 +c��A��0���أ�0���գ�0��ͼ���һ���֣�
+c��A��0���أ�0���գ�0��ͼ���һ���֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com