
(10分)设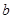 和
和 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量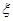 表示方程
表示方程
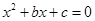 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(Ⅰ)求方程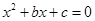 有实根的概率;
有实根的概率;
(Ⅱ)求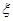 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程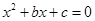 有实根的概率.
有实根的概率.
(Ⅰ)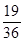
(Ⅱ)
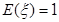
(Ⅲ)
【解析】本试题主要考查了古典概型概率的计算,以及分布列和数学期望的求解的综合运用。
(1)中理解本题是一个等可能事件的概率,试验发生包含的基本事件总数为6×6=36,那么借助于使方程有实根△=b2-4c≥0,得到事件A发生的基本事件数,得到概率值。
(2)利用ξ=0,1,2的可能取值,分别得到各个取值的概率值,然后写出分布列和数学期望值
(3)分析在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根,这是一个条件概率,利用条件概率公式得到结论。
解:(I)由题意知,本题是一个等可能事件的概率,
试验发生包含的基本事件总数为6×6=36,
满足条件的事件是使方程有实根,则△=b2-4c≥0,即.
下面针对于c的取值进行讨论
当c=1时,b=2,3,4,5,6; 当c=2时,b=3,4,5,6;
当c=3时,b=4,5,6; 当c=4时,b=4,5,6;
当c=5时,b=5,6; 当c=6时,b=5,6,
目标事件个数为5+4+3+3+2+2=19,
因此方程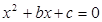 有实根的概率为
有实根的概率为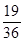
(II)由题意知用随机变量ξ表示方程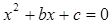 实根的个数得到
实根的个数得到
ξ=0,1,2 根据第一问做出的结果得到
则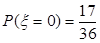 ,
,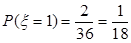 ,
,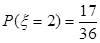 ,
,
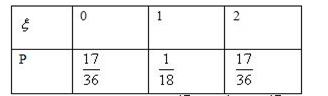
∴ξ的分布列为
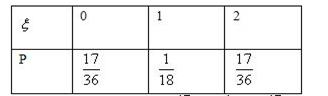
∴ξ的数学期望 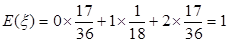
(III)在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根,
这是一个条件概率,
记“先后两次出现的点数中有5”为事件M,
“方程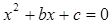 有实根”为事件N,
有实根”为事件N,
则,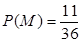 ,
,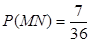 ∴
∴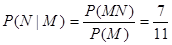


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
 选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).
选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).
|
| π |
| 4 |
| ||
| 2 |
| ab |
| bc |
| ca |
查看答案和解析>>
科目:高中数学 来源:2011年福建省罗源县第一中学高一上学期期中考试数学 题型:解答题
((本题13分)汽车和自行车分别从A地和C地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米。(汽车开到C地即停止)
(1)经过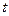 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为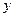 ,写出
,写出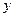 关于
关于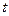 的函数关系式,并求出定义域。
的函数关系式,并求出定义域。
(2)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?
查看答案和解析>>
科目:高中数学 来源:2011年福建省高一上学期期中考试数学 题型:解答题
((本题13分)汽车和自行车分别从A地和C地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米。(汽车开到C地即停止)
(1)经过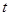 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为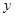 ,写出
,写出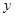 关于
关于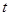 的函数关系式,并求出定义域。
的函数关系式,并求出定义域。
(2)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?

查看答案和解析>>
科目:高中数学 来源:2010年大连市高二下学期六月月考理科数学卷 题型:解答题
(本题满分10分) 设 和
和 分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程
分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程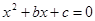 的实根的个数(重根按一个计)。
的实根的个数(重根按一个计)。
(1)求方程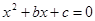 有实根的概率;(2)求随机变量X的分布列和数学期望;
有实根的概率;(2)求随机变量X的分布列和数学期望;
(3)若 中至少有一个为3,求方程
中至少有一个为3,求方程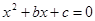 有实根的概率。
有实根的概率。
查看答案和解析>>
科目:高中数学 来源:江苏省南通市通州区2010届高三下学期查漏补缺专题训练(理) 题型:解答题
(选做题)从A,B,C,D四个中选做2个,每题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.
 A.(本小题为选做题,满分10分)
A.(本小题为选做题,满分10分)
如图,AB是半圆的直径,C是AB延长线上一点,CD
切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是
OB的中点,求BC的长.
B.(本小题为选做题,满分10分)
已知矩阵 ,其中
,其中 ,若点P(1,1)在矩阵A的变换下得到点
,若点P(1,1)在矩阵A的变换下得到点 ,
,
(1)求实数a的值; (2)求矩阵A的特征值及特征向量.
C.(本小题为选做题,满分10分)
设点 分别是曲线
分别是曲线 和
和 上的动点,求动点
上的动点,求动点 间的最小距离.
间的最小距离.
D.(本小题为选做题,满分10分)
设 为正数,证明:
为正数,证明: ≥
≥ .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com