
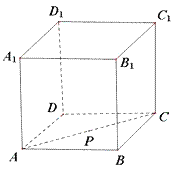
【题目】如图,在正方体ABCD﹣A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题:
①D1P∥平面A1BC1;
②D1P⊥BD;
③平面PDB1⊥平面A1BC1;
④三棱锥A1﹣BPC1的体积不变.
则其中所有正确的命题的序号是_____.
【答案】①③④
【解析】
利用线面平行的判定定理与性质定理,面面垂直的判定定理与三棱锥的体积公式对四个选项逐一分析判断即可.
①∵在正方体中,D1A∥BC1,D1C∥BA1,且D1A∩DC1=D1,∴平面D1AC∥平面A1BC1;∵P在面对角线AC上运动,∴D1P∥平面A1BC1;∴①正确.
②当P位于AC的中点时,D1P⊥BD不成立,∴②错误;
③∵A1C1⊥平面BDD1B1;∴A1C1⊥B1D,同理A1B⊥B1D,∴B1D⊥平面A1BC1,∴平面BDD1B⊥面ACD1,∴平面PDB1⊥平面A1BC1;∴③正确.
④三棱锥A1-BPC1的体积等于B-A1PC1的体积,△A1PC1的面积为定值![]() A1C1AA1,B到平面A1PC1的高为BP为定值,∴三棱锥A1-BPC1的体积不变,∴④正确.
A1C1AA1,B到平面A1PC1的高为BP为定值,∴三棱锥A1-BPC1的体积不变,∴④正确.
故答案为:①③④.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线![]() 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点![]() .
.
(1)若![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值;
的值;
(2)设线段![]() 的中点为
的中点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过
,过![]() 的直线
的直线![]() 与线段
与线段![]() 为直径的圆相切,切点为
为直径的圆相切,切点为![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为矩形,侧棱PA⊥底面ABCD,且PA=AD,E,F分别是线段PA,PD的中点,H在线段AB上.
(1)求证:PC⊥AF;
(2)若平面PBC∥平面EFH,求证H是AB的中点;
(3)若AD=4,AB=2,求点D到平面PAC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC= ![]() AB=
AB= ![]() ,平面PBC⊥平面ABCD.
,平面PBC⊥平面ABCD. 
(1)求证:AC⊥PB;
(2)若PB=PC= ![]() ,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为
,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com