
| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
分析 由题意,直线的方程为y=$\sqrt{3}$(x-2),代入y2=8x可得3x2-20x+12=0,求出A,B的坐标,再求出C的坐标,即可求出$\frac{{S}_{△AOC}}{{S}_{△BOF}}$.
解答 解:由题意,直线的方程为y=$\sqrt{3}$(x-2),
代入y2=8x可得3x2-20x+12=0,∴x=6或$\frac{2}{3}$,
∴A(6,4$\sqrt{3}$),B($\frac{2}{3}$,$\frac{4\sqrt{3}}{3}$),
又抛物线的准线方程为x=-2,∴C(-2,-4$\sqrt{3}$),
∴$\frac{{S}_{△AOC}}{{S}_{△BOF}}$=$\frac{\frac{1}{2}•2•8\sqrt{3}}{\frac{1}{2}•2•\frac{4\sqrt{3}}{3}}$=6,
故选:A.
点评 本题考查直线与抛物线的位置关系,考查抛物线的性质,考查三角形面积的计算,确定A,B,C的坐标是关键.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{12}$ | C. | $\frac{7\sqrt{3}}{12}$ | D. | -$\frac{7\sqrt{3}}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
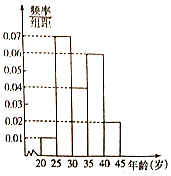 今年我国许多省市雾霾频发,为增强市民的环境保护意识,某市面向全市学校征召100名教师做义务宣传志愿者,成立环境保护宣传组,现把该组的成员按年龄分成5组:第一组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.
今年我国许多省市雾霾频发,为增强市民的环境保护意识,某市面向全市学校征召100名教师做义务宣传志愿者,成立环境保护宣传组,现把该组的成员按年龄分成5组:第一组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 3 | C. | 15 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com