
【题目】如图所示,在四棱锥![]() 中,
中,![]() 是正方形,
是正方形,![]() 平面
平面![]() ,
, ![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
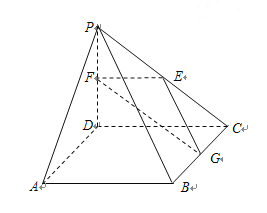
(1)求证:平面![]() 平面
平面![]() ;
;
(2)证明平面![]() 平面
平面![]() ,并求出
,并求出![]() 到平面
到平面![]() 的距离.
的距离.
科目:高中数学 来源: 题型:
【题目】退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势.某机构为了解某城市市民的年龄构成,按![]() 的比例从年龄在20~80岁(含20岁和80岁)之间的市民中随机抽取600人进行调查,并将年龄按
的比例从年龄在20~80岁(含20岁和80岁)之间的市民中随机抽取600人进行调查,并将年龄按![]() 进行分组,绘制成频率分布直方图,如图所示.规定年龄在
进行分组,绘制成频率分布直方图,如图所示.规定年龄在![]() 岁的人为“青年人”,
岁的人为“青年人”,![]() 岁的人为“中年人”,
岁的人为“中年人”, ![]() 岁的人为“老年人”.
岁的人为“老年人”.

(Ⅰ)根据频率分布直方图估计该城市60岁以上(含60岁)的人数,若每一组中的数据用该组区间的中点值来代表,试估算所调查的600人的平均年龄;
(Ⅱ)将上述人口分布的频率视为该城市年龄在20~80岁的人口分布的概率,从该城市年龄在20~80岁的市民中随机抽取3人,记抽到“老年人”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①已知![]() ,“
,“![]() 且
且![]() ”是“
”是“![]() ”的充分条件;
”的充分条件;
②已知平面向量![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③已知![]() ,“
,“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
④命题![]() :“
:“![]() ,使
,使![]() 且
且![]() ”的否定为
”的否定为![]() :“
:“![]() ,都有
,都有![]() 且
且![]() ”.其中正确命题的个数是( )
”.其中正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举办数学知识竞赛活动,共5000名学生参加,竞赛分为初试和复试,复试环节共3道题,其中2道单选题,1道多选题,得分规则如下:参赛学生每答对一道单选题得2分,答错得O分,答对多选题得3分,答错得0分,答完3道题后的得分之和为参赛学生的复试成绩.
(1)通过分析可以认为学生初试成绩![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() ,
,![]() ,试估计初试成绩不低于90分的人数;
,试估计初试成绩不低于90分的人数;
(2)已知小强已通过初试,他在复试中单选题的正答率为![]() ,多选题的正答率为
,多选题的正答率为![]() ,且每道题回答正确与否互不影响.记小强复试成绩为
,且每道题回答正确与否互不影响.记小强复试成绩为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“剪刀、石头、布”的游戏规则是:双方齐喊口令,然后同时出拳,握紧的拳头代表“石头”,“食指和中指伸出代表“剪刀”,五指伸开代表“布”。“ 石头”胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”,若所出拳相同则为和局。现甲乙两人通过“剪刀、石头、布”进行比赛。
(1)设甲乙两人每局都随机出“剪刀”、“石头”、“布”中的某一个,求甲胜乙的概率;
(2)最近中国科学家在网上发布了“剪刀、石头、布”的致胜策略,引起了甲的关注,据甲认真观察,乙有以下出拳习惯:①第一局不出“剪刀”; ②连续两局的出拳一定不一样,即如本局出“剪刀”,则下局出“石头”、“布”中的一个。假设甲的分析是正确的,甲据此分析出拳,保证每局都不输给乙,在最多5局的比赛中,谁胜的局数多,谁获胜。游戏结束的条件是:一方胜3局或赛满5局,用![]() 表示游戏结束时的游戏局数,求
表示游戏结束时的游戏局数,求![]() 的分布列和期望。
的分布列和期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]()
(1)若![]() ,且
,且![]() 在其定义域上存在单调递减区间,求实数
在其定义域上存在单调递减区间,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() ,
, ![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() 、
、![]() ,过线段
,过线段![]() 的中点作
的中点作![]() 轴的垂线分别交
轴的垂线分别交![]() ,
, ![]() 于点
于点![]() 、
、![]() ,证明:
,证明: ![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线不平行.
处的切线不平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了加强学生数学核心素养的培养,锻炼学生自主探究的学习能力,他们以函数![]() 为基本素材研究该函数的相关性质,某研究小组6位同学取得部分研究成果如下:
为基本素材研究该函数的相关性质,某研究小组6位同学取得部分研究成果如下:
①同学甲发现:函数![]() 的零点为
的零点为![]() ;
;
②同学乙发现:函数![]() 是奇函数;
是奇函数;
③同学丙发现:对于任意的![]() 都有
都有![]() ;
;
④同学丁发现:对于任意的![]() ,都有
,都有![]() ;
;
⑤同学戊发现:对于函数![]() 定义域中任意的两个不同实数
定义域中任意的两个不同实数![]() ,
,![]() ,总满足
,总满足![]() ;
;
⑥同学己发现:求使![]() 的x的取值范围是
的x的取值范围是![]() .
.
其中正确结论的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com