
【题目】已知椭圆 ![]()
![]() 经过点
经过点 ![]() ,其离心率
,其离心率 ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)设动直线 ![]() 与椭圆
与椭圆 ![]() 相切,切点为
相切,切点为 ![]() ,且
,且 ![]() 与直线
与直线 ![]() 相交于点
相交于点 ![]() .
.
试问:在 ![]() 轴上是否存在一定点,使得以
轴上是否存在一定点,使得以 ![]() 为直径的圆恒过该定点?若存在,
为直径的圆恒过该定点?若存在,
求出该点的坐标;若不存在,请说明理由.
 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据,
(吨标准煤)的几组对照数据,

(1)求![]() ,
, ![]() ,
,
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技动前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
已知![]() ,
, ![]() .
.
 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建设美丽乡村,政府欲将一块长12百米,宽5百米的矩形空地ABCD建成生态休闲园,园区内有一景观湖EFG(图中阴影部分),以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系xOy(如图所示).景观湖的边界线符合函数y=x+ ![]() (x>0)模型,园区服务中心P在x轴正半轴上,PO=
(x>0)模型,园区服务中心P在x轴正半轴上,PO= ![]() 百米.
百米. 
(1)若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM,求OM的最短长度;
(2)若在线段DE上设置一园区出口Q,试确定Q的位置,使通道PQ最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 数列{bn}是等比数列,满足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 .
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)令Cn= 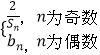 设数列{cn}的前n项和Tn , 求T2n .
设数列{cn}的前n项和Tn , 求T2n .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某淘宝商城在2017年前7个月的销售额![]() (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知![]() 与
与![]() 具有较好的线性关系.
具有较好的线性关系. 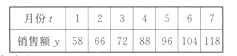
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
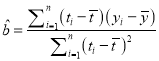 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M={x||x|<1},N={y|y=2x , x∈M},则集合R(M∩N)等于( )
A.(﹣∞, ![]() ]
]
B.( ![]() ,1)
,1)
C.(﹣∞, ![]() ]∪[1,+∞)
]∪[1,+∞)
D.[1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com