
【题目】已知函数![]() .
.
(1)若函数![]() 与
与![]() 的图象上存在关于原点对称的点,求实数
的图象上存在关于原点对称的点,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,已知
,已知![]() 在
在![]() 上存在两个极值点
上存在两个极值点![]() ,且
,且![]() ,求证:
,求证:![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,下列判断正确的是( )
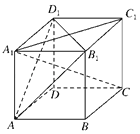
A.A1C⊥面AB1D1B.A1C⊥面AB1C1D
C.A1B⊥面AB1D1D.A1B⊥AD1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 的定义域为
的定义域为![]() ,且存在实常数
,且存在实常数![]() ,使得对于定义域内任意
,使得对于定义域内任意![]() ,都有
,都有![]() 成立,则称此函数
成立,则称此函数![]() 具有“性质
具有“性质![]() ”.
”.
(1)判断函数![]() 是否具有“
是否具有“![]() 性质”,若具有“
性质”,若具有“![]() 性质”,求出所有
性质”,求出所有![]() 的值的集合,若不具有“
的值的集合,若不具有“![]() 性质”,请说明理由;
性质”,请说明理由;
(2)已知函数![]() 具有“
具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(3)已知函数![]() 既具有“
既具有“![]() 性质”,又具有“
性质”,又具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,若函数
,若函数![]() 的图像与直线
的图像与直线![]() 有2017个公共点,求实数
有2017个公共点,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种零件的质量指标值以分数(满分100分)衡量,并根据分数的高低划分三个等级,如下表:

为了监控某种零件的一条生产线的生产过程,检验员随机抽取了100件零件,进行质量指标值检查,将检查结果进行整理得到如下的频率分布直方图:
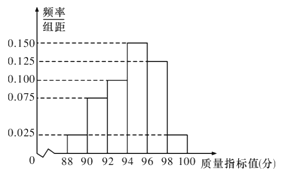
(1)若该生产线的质量指标值要求为:
第一条:生产线的质量指标值合格和优秀的零件至少要占全部零件的75%,
第二条:生产线的质量指标值平均分不低于95分;
如果同时满足以上两条就认定生产线的质量指标值合格,否则为不合格,请根据以上抽样调查数据,判断该生产线的质量指标值是否合格?
(2)在样本中,按质量指标值的等级用分层抽样的方法从质量指标值不合格和优秀的零件中抽取5件,再从这5件中随机抽取2件,求这两件的质量指标值恰好一个不合格一个优秀的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-2x-3≤0},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若ARB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是( )
游戏1 | 游戏2 | 游戏3 |
袋中装有一个红球和一个白球 | 袋中装有2个红球和2个白球 | 袋中装有3个红球和1个白球 |
取1个球, | 取1个球,再取1个球 | 取1个球,再取1个球 |
取出的球是红球→甲胜 | 取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
A.游戏1B.游戏2C.游戏3D.游戏2和游戏3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为公司在2017年8月9日推出的一款手机,已于9月19日正式上市.据统计发现该产品的广告费用x与销售额y的统计数据如下表:
广告费用x(百万元) | 4 | 2 | 3 | 5 |
销售额y(百万元) | 44 | 25 | 37 | 54 |
根据上表可得回归方程![]() 中的
中的![]() 为9.4,据此模型预测广告费用为6百万元时,销售额为( )
为9.4,据此模型预测广告费用为6百万元时,销售额为( )
A.61.5百万元B.62.5百万元C.63.5百万元D.65.0百万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com