练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知为奇函数，为偶函数，且.

    （1）求及的解析式及定义域；

    （2）若函数在区间上为单调函数，求实数k的范围；

    （3）若关于x的方程有解，求实数m的取值范围.

    【答案】（1），；（2）；（3）

    【解析】

    （1）根据奇偶性得到方程组和，计算得到答案.

    （2）化简得到，根据开口方向和对称轴计算得到答案.

    （3）化简得到，设计算得到，得到，计算得到答案.

    （1）因为是奇函数，是偶函数，所以，．

    因为，①所以用-x取代x代入上式得

    ，即，②

    联立①②可得，，

    ．

    （2）因为，所以，

    因为函数在区间上为单调函数，所以或，

    所以所求实数k的取值范围为．

    （3）因为，所以．设，

    则．因为的定义域为，，

    所以，，，，即，则．

    因为关于x的方程有解，则，

    故m的取值范围为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，且．

    (1)判断函数的奇偶性；

    (2) 判断函数在(1，＋∞)上的单调性，并用定义证明你的结论；

    (3)若，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题：，命题：

    （1）若是的充分条件，求实数的取值范围；

    （2）若，为真命题，为假命题，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】高三一班、二班各有6名学生去参加学校组织的高中数学竞赛选拔考试，成绩如茎叶图所示.

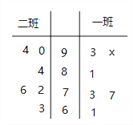
    （1）若一班、二班6名学生的平均分相同，求值；

    （2）若将竞赛成绩在、、内的学生在学校推优时，分别赋分、2分、3分，现在从一班的6名参赛学生中选两名，求推优时，这两名学生赋分的和为4分的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下判断正确的是 （ ）

    A. 函数为上的可导函数，则是为函数极值点的充要条件

    B. 若命题为假命题，则命题与命题均为假命题

    C. 若，则的逆命题为真命题

    D. 在中，“”是“”的充要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （Ⅰ）当时， 取得极值，求的值；

    （Ⅱ）当函数有两个极值点，且时，总有 成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】目前，某市出租车的计价标准是：路程以内（含）按起步价8元收取，超过后的路程按1.9元收取，但超过后的路程需加收的返空费（即单价为元）

    （1）若，将乘客搭乘一次出租车的费用（单位：元）表示为行程（单位：）的分段函数；

    （2）某乘客行程为，他准备先乘一辆出租车行驶，然后再换乘另一辆出租车完成余下路程，请问：他这样做是否比只乘一辆出租车完成全程更省钱？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义域为的函数满足：对于任意的实数都有 成立，且当时，．

    （Ⅰ）判断函数的奇偶性，并证明你的结论；

    （Ⅱ）证明在上为减函数；

    （Ⅲ）若，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其图像与轴切于非原点的一点，且该函数的极小值是，那么切点坐标为______．

    查看答案和解析>>

    同步练习册答案