
【题目】甲、乙两个人独立地破译一个密码,他们能译出密码的概率分别为![]() 和
和![]() .
.
(1)求2个人都译出密码的概率;
(2)求2个人都译不出密码的概率;
(3)求至多1个人都译出密码的概率;
(4)求至少1个人都译出密码的概率.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]()
【解析】
(1)利用独立事件同时发生的概率乘法公式可求;
(2)先求解两人不能译出密码的概率,结合独立事件概率乘法公式可求;
(3)利用对立事件进行求解,“至多1个人译出密码”的对立事件为“2个人都译出密码”;
(4)利用对立事件进行求解,“至少1个人译出密码”的对立事件为“2个人都未译出密码”.
(1)记“甲独立地译出密码”事件![]() ,“乙独立地译出密码”为事件
,“乙独立地译出密码”为事件![]() ,且
,且![]() ,
,![]() 为相互独立事件,且
为相互独立事件,且![]() ,
,![]() .
.
2个人都译出密码的概率为
![]() .
.
(2)2个人都译不出密码的概率为
![]() .
.
(3)“至多1个人译出密码”的对立事件“2个人都译出密码”,所以至多1个人译出密码的概率为
![]() .
.
(4)“至少1个人译出密码”的对立事件“2个人都未译出密码”,所以至少1个人译出密码的概率为
![]() .
.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】如图所示,将四棱锥S-ABCD的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种色可供使用,则不同的染色方法种数为( )
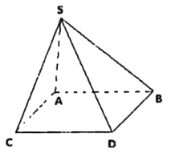
A.240B.360C.420D.960
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某省各景点在大众中的熟知度,随机对15~65岁的人群抽样了![]() 人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组 | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|

(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机支付也称为移动支付![]() ,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
组数 | 第l组 | 第2组 | 第3组 | 第4组 | 第5组 |
分组 |
|
|
|
|
|
频数 | 20 | 36 | 30 | 10 | 4 |
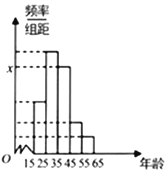
(1)求![]() ;
;
(2)从第l,3,4组中用分层抽样的方法抽取6人,求第l,3,4组抽取的人数:
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示. 已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16 .

(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查, 问应在第三批次中抽取教职工多少名?
(3)已知![]() ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类比平面几何中的定理:△ABC中,若DE是△ABC的中位线,则有S△ADE∶S△ABC=1∶4;若三棱锥A-BCD有中截面EFG∥平面BCD,则截得三棱锥的体积与原三棱锥体积之间的关系式为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com