
| A. | V=$\frac{1}{3}$abc(a,b,c,为底面边长) | |
| B. | V=$\frac{1}{3}$Sh(S为底面面积,h为四面体的高) | |
| C. | V=$\frac{1}{3}$(S1+S2+S3+S4)r(S1,S2,S3,S4分别为四面体四个面的面积,r为四面 体内切球的半径) | |
| D. | V=$\frac{1}{3}$(ab+bc+ac)h(a,b,c为底面边长,h为四面体的高) |
分析 根据平面与空间之间的类比推理,由点类比点或直线,由直线 类比 直线或平面,由内切圆类比内切球,由平面图形面积类比立体图形的体积,结合求三角形的面积的方法类比求四面体的体积即可.
解答 解:设四面体的内切球的球心为O,则球心O到四个面的距离都是r,
根据三角形的面积的求解方法:分割法,将O与四顶点连起来,可得四面体的体积等于以O为顶点,分别以四个面为底面的4个三棱锥体积的和,
∴V=$\frac{1}{3}$(S1+S2+S3+S4)r,
故选C.
点评 类比推理是指依据两类数学对象的相似性,将已知的一类数学对象的性质类比迁移到另一类数学对象上去.一般步骤:①找出两类事物之间的相似性或者一致性.②用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(或猜想).


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:选择题
| A. | x2=2y | B. | x2=4y | C. | x2=2y或x2=4y | D. | x2=3y或x2=2y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=-3,b=1 | B. | a=3,b=1 | C. | a=-3,b=-1 | D. | a=3,b=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
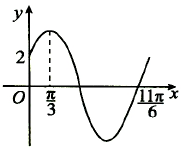 已知函数$f(x)=Asin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ② | B. | ①② | C. | ③④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲日德、乙法德、丙英法、丁英德 | B. | 甲日英、乙日德、丙德法、丁日英 | ||
| C. | 甲日德、乙法德、丙英德、丁英德 | D. | 甲日法、乙英德、丙法德、丁法英 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com