
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,直线l:
(θ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,直线l: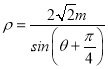 (m为常数).
(m为常数).
(1)求曲线C的普通方程与直线l的直角坐标方程;
(2)若直线l与曲线C相交于A、B两点,当|AB|=4时,求实数m的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,左右焦点分别为
轴上,左右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,右焦点到右顶点的距离为1.
,右焦点到右顶点的距离为1.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,则
,则![]() 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,又函数![]() .
.
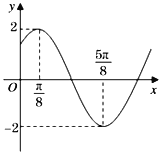
(1)求函数![]() 的单调减区间;
的单调减区间;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,又![]() ,且锐角C满足
,且锐角C满足![]() ,若sinB=2sinA,求a+b的值.
,若sinB=2sinA,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2AD=4,过AA1作平面α使BD⊥α,且平面α∩平面A1B1C1D1=l,M∈l.下面给出了四个命题:这四个命题中,真命题的个数为( )
①l∥AC;
②BM⊥AC;
③l和AD1所成的角为60°;
④线段BM长度的最小值为![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲,乙两地某月![]() 时的气温,随机选取该月中的
时的气温,随机选取该月中的![]() 天,将这
天,将这![]() 天中
天中![]() 时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:①甲地该月
时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:①甲地该月![]() 时的平均气温低于乙地该月
时的平均气温低于乙地该月![]() 时的平均气温;②甲地该月
时的平均气温;②甲地该月![]() 时的平均气温高于乙地该月
时的平均气温高于乙地该月![]() 时的平均气温;③甲地该月
时的平均气温;③甲地该月![]() 时的气温的中位数小于乙地该月
时的气温的中位数小于乙地该月![]() 时的气温的中位数;④甲地该月
时的气温的中位数;④甲地该月![]() 时的气温的中位数大于乙地该月
时的气温的中位数大于乙地该月![]() 时的气温的中位数.其中根据茎叶图能得到的正确结论的编号为( )
时的气温的中位数.其中根据茎叶图能得到的正确结论的编号为( )

A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学的期末考试中抽取部分学生的数学成绩,由抽查结果得到如图的频率分布直方图,分数落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
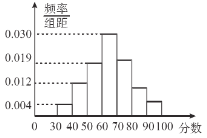
(1)求这些学生的分数落在区间![]() 内的频率;
内的频率;
(2)(ⅰ)若采用分层抽样的方法从分数落在区间![]() ,
,![]() 内抽取4人,求从分数落在区间
内抽取4人,求从分数落在区间![]() ,
,![]() 内各抽取的人数;
内各抽取的人数;
(ⅱ)从上述抽取的4人中再随机抽取2人,求这2人全部来自于区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,其焦点到准线的距离为2.直线
,其焦点到准线的距离为2.直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 与
与![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com