
[番茄花园1] 本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分10分。
若实数 、
、 、
、 满足
满足 ,则称
,则称 比
比 远离
远离 .
.
(1)若 比1远离0,求
比1远离0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、 ,证明:
,证明: 比
比 远离
远离 ;
;
(3)已知函数 的定义域
的定义域 .任取
.任取 ,
, 等于
等于 和
和 中远离0的那个值.写出函数
中远离0的那个值.写出函数 的解析式,并指出它的基本性质(结论不要求证明).
的解析式,并指出它的基本性质(结论不要求证明).
23本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知椭圆 的方程为
的方程为 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).
(1)若直角坐标平面上的点M、A(0,-b),B(a,0)满足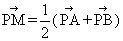 ,求点
,求点 的坐标;
的坐标;
(2)设直线 交椭圆
交椭圆 于
于 、
、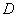 两点,交直线
两点,交直线 于点
于点 .若
.若 ,证明:
,证明: 为
为 的中点;
的中点;
(3)对于椭圆 上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆
上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆 上存在不同的两个交点
上存在不同的两个交点 、
、 满足
满足 ,写出求作点
,写出求作点 、
、 的步骤,并求出使
的步骤,并求出使 、
、 存在的θ的取值范围.
存在的θ的取值范围.
[番茄花园1]22.
[番茄花园1] 解析:(1) 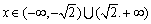 ;
;
(2) 对任意两个不相等的正数a、b,有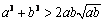 ,
,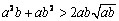 ,
,
因为 ,
,
所以 ,即a3+b3比a2b+ab2远离
,即a3+b3比a2b+ab2远离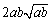 ;
;
(3)  ,
,
性质:1°f(x)是偶函数,图像关于y轴对称,2°f(x)是周期函数,最小正周期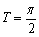 ,
,
3°函数f(x)在区间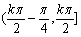 单调递增,在区间
单调递增,在区间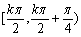 单调递减,kÎZ,
单调递减,kÎZ,
4°函数f(x)的值域为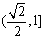 .
.
23解析:(1)  ;
;
(2) 由方程组 ,消y得方程
,消y得方程 ,
,
因为直线 交椭圆
交椭圆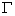 于
于 、
、 两点,
两点,
所以D>0,即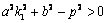 ,
,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x0,y0),
则 ,
,
由方程组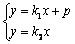 ,消y得方程(k2-k1)x=p,
,消y得方程(k2-k1)x=p,
又因为 ,所以
,所以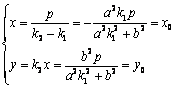 ,
,
故E为CD的中点;
(3) 求作点P1、P2的步骤:1°求出PQ的中点 ,
,
2°求出直线OE的斜率 ,
,
3°由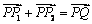 知E为CD的中点,根据(2)可得CD的斜率
知E为CD的中点,根据(2)可得CD的斜率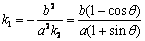 ,
,
4°从而得直线CD的方程: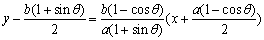 ,
,
5°将直线CD与椭圆Γ的方程联立,方程组的解即为点P1、P2的坐标.
欲使P1、P2存在,必须点E在椭圆内,
所以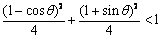 ,化简得
,化简得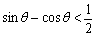 ,
,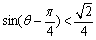 ,
,
又0<q <p,即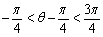 ,所以
,所以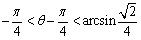 ,
,
故q 的取值范围是 .
.
[番茄花园1]22.


 口算题天天练系列答案
口算题天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com