
分析 (1)两次投球恰好命中一次包括两种情况,即甲能够命中而乙不能命中,或甲不能命中而乙能够命中,这两种情况是互斥的.根据相互独立事件和互斥事件的概率公式得到结果.
(2)四次投球中至少有一次命中的对立事件是四次投球一次也不能命中,首先根据相互独立事件同时发生的概率做出一次也不能命中的概率,再用对立事件的概率公式得到结果.
解答 解:(1)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事B,
则P(A)=$\frac{1}{2}$,P(B)=$\frac{2}{5}$,P($\overline{A}$)=$\frac{1}{2}$,P($\overline{B}$)=$\frac{3}{5}$.
甲、乙两人在罚球线各投球一次,恰好命中一次的事件为A$\overline{B}$+B$\overline{A}$,
P(A$\overline{B}$+B$\overline{A}$)=$\frac{1}{2}$×$\frac{3}{5}$+$\frac{2}{5}$×$\frac{1}{2}$=$\frac{1}{2}$,
∴甲、乙两人在罚球线各投球一次,求恰好命中一次的概率为$\frac{1}{2}$;
(2)∵事件“甲、乙两人在罚球线各投球二次全不命中”的概率是
P′=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{3}{5}$×$\frac{3}{5}$=$\frac{9}{100}$,
∴甲、乙两人在罚球线各投球二次,至少有一次命中的概率为
P=1-$\frac{9}{100}$=$\frac{91}{100}$,
∴甲、乙两人在罚球线各投球二次,至少有一次命中的概率为$\frac{91}{100}$.
点评 本题看出相互独立事件同时发生的概率和对立事件的概率,本题解题的关键是看清题目中所求的事件的概率的意义,正面来解释比较困难,可以选择应用对立事件来解决.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overline{y}$=1.5$\overline{x}$-15 | B. | 15是回归系数a | ||
| C. | 1.5是回归系数a | D. | 当x=10时,y的准确值为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6和2.4 | B. | 6和5.6 | C. | 2和5.6 | D. | 2和2.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
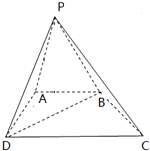 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com