
【题目】设![]() 是一个给定的非零实数,在平面直角坐标系
是一个给定的非零实数,在平面直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() 且
且![]() ,点
,点![]() .
.
(1)设![]() 是
是![]() 上的任意一点,试求线段
上的任意一点,试求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程并指出曲线
的方程并指出曲线![]() 的类型和位置;
的类型和位置;
(2)求出![]() 、
、![]() 在它们的交点
在它们的交点![]() 处的各自切线之间的夹角
处的各自切线之间的夹角![]() (锐角)(用反三角函数式表示)
(锐角)(用反三角函数式表示)
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上任意一点
上任意一点![]() 到直线
到直线![]() 的距离是它到点
的距离是它到点![]() 距离的2倍;曲线
距离的2倍;曲线![]() 是以原点为顶点,
是以原点为顶点,![]() 为焦点的抛物线.
为焦点的抛物线.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() 两点,分别以
两点,分别以![]() 为切点引曲线
为切点引曲线![]() 的两条切线
的两条切线![]() ,设
,设![]() 相交于点
相交于点![]() ,连接
,连接![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色、相邻区域颜色不同,则区域不同涂色的方法种数为( )
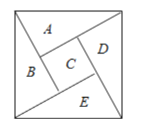
A.360B.400C.420D.480
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.
(1)求抛物线方程;
(2)直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试问:能否把2008表示成![]() 的形式?如果可以,这种表示方式是否有无限多个?其中,m、n均为大于100且小于170的正整数,且
的形式?如果可以,这种表示方式是否有无限多个?其中,m、n均为大于100且小于170的正整数,且![]() ;
;![]() 均为两两不相等的小于6的正有理数,且
均为两两不相等的小于6的正有理数,且![]() 均为大于1且小于5的正整数,同时,
均为大于1且小于5的正整数,同时, ![]() 两两不相等,
两两不相等,![]() 也两两不相等请说明理由.
也两两不相等请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x![]() ,g(x)=2x+a,若x1∈[
,g(x)=2x+a,若x1∈[![]() ,1],x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是( )
,1],x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是( )
A.a≤1B.a≥1C.a≤2D.a≥2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】推进垃圾分类处理,是落实绿色发展理念的必然选择,也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度,某社区居委会随机抽取1000名社区居民参与问卷测试,并将问卷得分绘制频率分布表如表:
得分 |
|
|
|
|
|
|
|
男性 人数 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性 人数 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)从该社区随机抽取一名居民参与问卷测试,试估计其得分不低于60分的概率;
(2)将居民对垃圾分类的了解程度分为“比较了解”(得分不低于60分)和“不太了解”(得分低于60分)两类,完成2×2列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
不太了解 | 比较了解 | 合计 | |
男性 | |||
女性 | |||
合计 |
(3)从参与问卷测试且得分不低于80分的居民中,按照性别进行分层抽样,共抽取10人,现从这10人中随机抽取3人作为环保宣传队长,设3人中男性队长的人数为ξ,求ξ的分布列和期望.
附:![]()
![]() ,(n=a+b+c+d).
,(n=a+b+c+d).
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是一个各位数字都不是0且没有重复数字的三位数,将组成
是一个各位数字都不是0且没有重复数字的三位数,将组成![]() 的3个数字按从小到大排成的三位数记为
的3个数字按从小到大排成的三位数记为![]() ,按从大到小排成的三位数记为
,按从大到小排成的三位数记为![]() ,(例如
,(例如![]() ,则
,则![]() ,
,![]() )阅读如图所示的程序框图,运行相应的程序,任意输入一个
)阅读如图所示的程序框图,运行相应的程序,任意输入一个![]() ,输出的结果
,输出的结果![]() =( )
=( )

A. 693 B. 594 C. 495 D. 792
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com