
【题目】如图抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线上一点(
为抛物线上一点(![]() 在
在![]() 轴上方),
轴上方),![]() ,
,![]() 点到
点到![]() 轴的距离为4.
轴的距离为4.
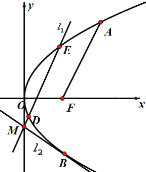
(1)求抛物线方程及点![]() 的坐标;
的坐标;
(2)是否存在![]() 轴上的一个点
轴上的一个点![]() ,过点
,过点![]() 有两条直线
有两条直线![]() ,满足
,满足![]() ,
,![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.![]() 与抛物线相切于点
与抛物线相切于点![]() (
(![]() 不为坐标原点),有
不为坐标原点),有![]() 成立,若存在,求出点
成立,若存在,求出点![]() 的坐标.若不存在,请说明理由.
的坐标.若不存在,请说明理由.
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】随着经济全球化信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争.吸引留住培养和用好人才成为人力资源管理的战略目标和紧迫任务.在此背景下,某信息网站在15个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如下图所示.
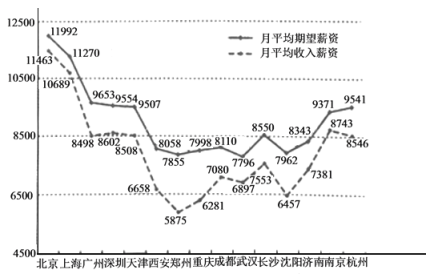
(1)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于8500元的城市的概率;
(2)若从月平均收入薪资与月平均期望薪资之差高于1000元的城市中随机选择2座城市,求这2座城市的月平均期望薪资都低于8500元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间生产甲、乙两种产品,已知制造一件甲产品需要![]() 种元件5个,
种元件5个,![]() 种元件2个,制造一件乙种产品需要
种元件2个,制造一件乙种产品需要![]() 种元件3个,
种元件3个,![]() 种元件3个,现在只有
种元件3个,现在只有![]() 种元件180个,
种元件180个,![]() 种元件135个,每件甲产品可获利润20元,每件乙产品可获利润15元,试问在这种条件下,应如何安排生产计划才能得到最大利润?
种元件135个,每件甲产品可获利润20元,每件乙产品可获利润15元,试问在这种条件下,应如何安排生产计划才能得到最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,
,![]() .
.
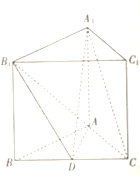
(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,试问:
,试问:![]() 是否与平面
是否与平面![]() 平行?若平行,求三棱锥
平行?若平行,求三棱锥![]() 的体积;若不平行,请说明理由.
的体积;若不平行,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立的极坐标系中,直线
轴的正半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为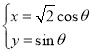 (
(![]() 为参数).
为参数).
(1)写出直线![]() 及曲线
及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且平行于直线
且平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,求点
,求点![]() 的轨迹及其直角坐标方程.
的轨迹及其直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com