
【题目】已知函数![]() .
.
(Ⅰ)求f(x)的最小正周期和单调递减区间;
(Ⅱ)将函数f(x)的图象向右平移![]() 个单位,得到函数g(x)的图象,求g(x)在区间
个单位,得到函数g(x)的图象,求g(x)在区间![]() 上的值域.
上的值域.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制得到下面的散点图.
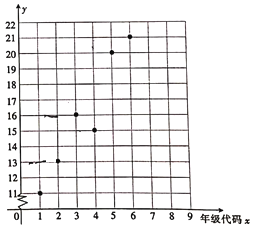
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
附注:参考数据:![]()
参考公式:相关系数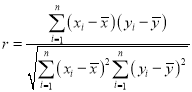 ,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为![]() =
=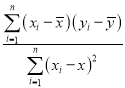 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂过去在生产过程中将污水直接排放到河流中对沿河环境造成了一定的污染,根据环保部门对该厂过去10年的监测数据,统计出了其每年污水排放量![]() (单位:吨)的频率分布表:
(单位:吨)的频率分布表:
污水排放量 |
|
|
|
|
频率 | 0.1 | 0.3 | 0.4 | 0.2 |
将污水排放量落入各组的频率作为概率,并假设每年该厂污水排放量相互独立.
(1)若不加以治理,根据上表中的数据,计算未来3年中至少有2年污水排放量不小于200吨的概率;
(2)根据环保部门的评估,该厂当年污水排放量![]() 时,对沿河环境及经济造成的损失为5万元;当年污水排放量
时,对沿河环境及经济造成的损失为5万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为10万元;当年污水排放量
时,对沿河环境及经济造成的损失为10万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为20万元;当年污水排放量
时,对沿河环境及经济造成的损失为20万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
方案1:若该厂不采取治污措施,则需全部赔偿对沿河环境及经济造成的损失;
方案2:若该厂采购治污设备对所有产生的污水净化达标后再排放,则不需赔偿,采购设备的费用为10万元,每年设备维护等费用为15万元,该设备使用10年需重新更换.在接下来的10年里,试比较上述2种方案哪种能为该厂节约资金,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某包子店每天早晨会提前做好若干笼包子,以保证当天及时供应,每卖出一笼包子的利润为40元,当天未卖出的包子作废料处理, 每笼亏损20元.该包子店记录了60天包子的日需求量![]() (单位:笼,
(单位:笼,![]() ),整理得到如图所示的条形图,以这60天各需求量的频率代替相应的概率.
),整理得到如图所示的条形图,以这60天各需求量的频率代替相应的概率.
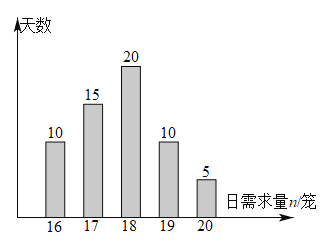
(1)设![]() 为一天的包子需求量,求
为一天的包子需求量,求![]() 的数学期望.
的数学期望.
(2)若该包子店想保证![]() 以上的天数能够足量供应,则每天至少要做多少笼包子?
以上的天数能够足量供应,则每天至少要做多少笼包子?
(3)为了减少浪费,该包子店一天只做18笼包子,设![]() 为当天的利润(单位:元),求
为当天的利润(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD所在平面垂直于直角梯形ABPE所在平面,EP![]() ,BP=2,AD=AE=1,AE⊥EP,AE∥BP,G,F分别是BP,BC的中点.
,BP=2,AD=AE=1,AE⊥EP,AE∥BP,G,F分别是BP,BC的中点.
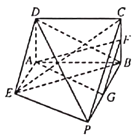
(1)求证:平面AFG∥平面PCE;
(2)求四棱锥D﹣ABPE的体积与三棱锥P﹣BCD的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的30个零件编号为01,02,…,19,30,现利用如下随机数表从中抽取5个进行检测. 若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件编号为( )
34 57 07 86 36 04 68 96 08 23 23 45 78 89 07 84 42 12 53 31 25 30 07 32 86 |
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,2Sn+2n=an+1﹣2,a2=8,其中n∈N*.
(1)记bn=an+1,求证:{bn}是等比数列;
(2)设![]() 为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com