练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数

    （1）求函数的值域；

    （2）若时，函数的最小值为，求的值和函数 的最大值.

    【答案】（1）值域为 ；（2）。

    【解析】

    试题（1）解本小题的关键是利用,把原函数转化为关于t的二次函数，的值域问题.（2）在（1）的基础上可确定在上是减函数,然后根据f(x)的最小值为-7,建立关于a的方程求出a值，从而得到函数f(x)的最大值.

    设

    （1）对称轴 在上是减函数

    所以值域为 ----------------------------------------- 6

    （2）∵ 由

    所以在上是减函数

    或（不合题意舍去）------------------------11

    当时有最大值，

    即 -----------------------------------------------13

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知关于x的方程为2kx2﹣2x﹣5k﹣2＝0的两个实数根一个小于1，另一个大于1，则实数k的取值范围是（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设全集U=R，集合A={x|2x-1≥1}，B={x|x2-4x-5＜0}．

    （Ⅰ）求A∩B，（UA）∪（UB）；

    （Ⅱ）设集合C={x|m+1＜x＜2m-1}，若B∩C=C，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正方形的棱长为1,点分别是棱的中点.

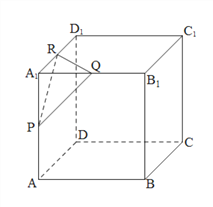
    （Ⅰ）求二面角的余弦值;

    （Ⅱ）以为底面作正三棱柱,若此三棱柱另一底面三个顶点也都在该正方体的表面上,求这个正三棱柱的高.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PPD//平面MAC，PA=PD=，AB=4．

    （I）求证：M为PB的中点；

    （II）求二面角B-PD-A的大小；

    （III）求直线MC与平面BDP所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知极点与直角坐标系的原点重合，极轴与x轴的正半轴重合，圆C的极坐标方程是ρ=asinθ，直线l的参数方程是 （t为参数）
    （1）若a=2，直线l与x轴的交点是M，N是圆C上一动点，求|MN|的最大值；
    （2）直线l被圆C截得的弦长等于圆C的半径的 倍，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lg（ax-bx）（a＞1＞b＞0）．

    （Ⅰ）求f（x）的定义域；

    （Ⅱ）当x∈（1，+∞）时，f（x）的值域为（0，+∞），且f（2）=lg2，求实数a、b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某食品企业一个月内被消费者投诉的次数用表示.据统计，随机变量的概率分布如下表所示.

    0

    1

    2

    3

    0.1

    0.3

    （1）求的值和的数学期望；

    （2）假设一月份与二月份被消费者投诉的次数互不影响，求该企业在这两个月内共被消费者投诉2次的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ex﹣ ，g（x）=2ln（x+1）+e﹣x ．
    （1）x∈（﹣1，+∞）时，证明：f（x）＞0；
    （2）a＞0，若g（x）≤ax+1，求a的取值范围．

    查看答案和解析>>

    同步练习册答案