
分析 (Ⅰ)由平面向量的坐标运算求出模长|$\overrightarrow{b}$+$\overrightarrow{c}$|,再根据三角函数的性质求出它的最大值;
(Ⅱ)根据平面向量的共线定理与数量积运算性质,求出tanαtanβ和tan(α+β)的值,即可求出tanα+tanβ的值.
解答 解:(Ⅰ)向量$\overrightarrow{b}$=(sinβ,4cosβ),$\overrightarrow{c}$=(cosβ,-4sinβ),
∴$\overrightarrow{b}$+$\overrightarrow{c}$=(sinβ+cosβ,4cosβ-4sinβ),…(2分)
∴|$\overrightarrow{b}$+$\overrightarrow{c}$|=$\sqrt{{(sinβ+cosβ)}^{2}{+(4cosβ-4sinβ)}^{2}}$=$\sqrt{17-15sin2β}$$≤\sqrt{32}=4\sqrt{2}$,
当且仅当$β=-\frac{π}{4}+kπ(k∈Z)$时取等号,…(5分)
∴|$\overrightarrow{b}$+$\overrightarrow{c}$|的最大值为$4\sqrt{2}$;…(6分)
(Ⅱ)向量$\overrightarrow{a}$=(4cosα,sinα),$\overrightarrow{b}$=(sinβ,4cosβ),
当$\overrightarrow{a}$∥$\overrightarrow{b}$时,16cosαcosβ-sinαsinβ=0,
∴tanαtanβ=16①;…(8分)
由 $\overrightarrow{a}$⊥($\overrightarrow{b}$-2$\overrightarrow{c}$),得 $\overrightarrow{a}$•($\overrightarrow{b}$-2$\overrightarrow{c}$)=0,
∴4cosα(sinβ-2cosβ)+sinα(4cosβ+8sinβ)=0,
∴sin(α+β)=2cos(α+β)…(11分)
∴tan(α+β)=2②;
由①②得:
tanα+tanβ=tan(α+β)(1-tanαtanβ)=2×(1-16)=-30.…(13分)
点评 本题考查了平面向量的坐标运算、模长公式以及三角函数的图象与性质的应用问题,是综合题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
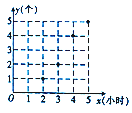 为确定加工某零件的时间,某工人做了四次实验,得到的数据的散点图如图所示.
为确定加工某零件的时间,某工人做了四次实验,得到的数据的散点图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥平面ABC,AC⊥BC,AC=1,BC=2,S,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥平面ABC,AC⊥BC,AC=1,BC=2,S,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正数 | B. | 负数 | C. | 零 | D. | 不能确定符号 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 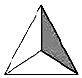 | B. | 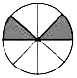 | C. | 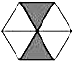 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com