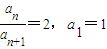分析:(1)①a
n=n-2,|a
n|=|n-2|≥0,n>2时数列单调递增,不存在实数T满足|a
n|≤T
②
an=>0且数列单调递减,则
|an|≤a1=,故存在T=
③
=2,a1=1可得
an=()n-1>0单调递减的数列,a
n≤a
1=1,存在T=1
(2)易知,a
n+1=-(a
n-1)
2+1由此得通项
an=1-(t-1)2n-1,由有界数列定义知,|t-1|≤1.结合t>0,可求t的范围
解答:解:(1)①a
n=n-2,|a
n|=|n-2|≥0,不存在实数T满足|a
n|≤T,①错误
②
an=>0且数列单调递减,则
|an|≤a1=,则T=
时,
|an|≤,②正确
③
=2,a1=1可得
an=()n-1>0单调递减的数列,a
n≤a
1=1,T=1时,|a
n|≤1,③正确
(2)∵a
n+1=-(a
n-1)
2+1≤1
∴1-a
n+1=(1-a
n)
2∴lg(1-a
n+1)=2lg(1-a
n)
即
=2由等比数列的通项公式可得,
an=1-(t-1)2n-1由有界数列定义知,|t-1|≤1.又t>0,故t的取值范围是0<t≤2.
故答案为:②③;0<t≤2
点评:本题主要考查了数列有界性的应用,实质是利用数列的单调性的定义求解数列的范围,解t的范围的关键是要求出数列的通项公式



 在同一直线l1上;
在同一直线l1上;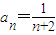 ③
③