
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 点
点![]() 是椭圆上任意一点,且
是椭圆上任意一点,且![]() 的最大值为4,椭圆
的最大值为4,椭圆![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
(1)求椭圆方程;
(2)设点![]() ,过点
,过点![]() 作直线
作直线![]() 与圆
与圆![]() 相切且分别交椭圆于
相切且分别交椭圆于![]() ,求直线
,求直线![]() 的斜率.
的斜率.
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是两个不重合的平面,在下列条件中,可判断平面
是两个不重合的平面,在下列条件中,可判断平面![]() ,
,![]() 平行的是( )
平行的是( )
A.![]() ,
,![]() 是平面
是平面![]() 内两条直线,且
内两条直线,且![]() ,
,![]()
B.![]() ,
,![]() 是两条异面直线,
是两条异面直线,![]() ,
,![]() ,且
,且![]() ,
,![]()
C.面![]() 内不共线的三点到
内不共线的三点到![]() 的距离相等
的距离相等
D.面![]() ,
,![]() 都垂直于平面
都垂直于平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的寒冷天气都会带热“御寒经济”,以餐饮业为例,当外面太冷时,不少人都会选择叫外卖上门,外卖商家的订单就会增加,下表是某餐饮店从外卖数据中抽取的5天的日平均气温与外卖订单数.
![]()
(Ⅰ)经过数据分析,一天内平均气温![]() 与该店外卖订单数
与该店外卖订单数![]() (份)成线性相关关系,试建立
(份)成线性相关关系,试建立![]() 关于
关于![]() 的回归方程,并预测气温为
的回归方程,并预测气温为![]() 时该店的外卖订单数(结果四舍五入保留整数);
时该店的外卖订单数(结果四舍五入保留整数);
(Ⅱ)天气预报预测未来一周内(七天),有3天日平均气温不高于![]() ,若把这7天的预测数据当成真实数据,则从这7天任意选取2天,求恰有1天外卖订单数不低于160份的概率.
,若把这7天的预测数据当成真实数据,则从这7天任意选取2天,求恰有1天外卖订单数不低于160份的概率.
附注:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: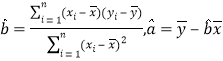 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了美化校园,要对校园内某一区域作如下设计,如图,已知![]() ,
,![]() ,
,![]() ,在边BC上选一点P. 沿着AP和CP重新栽种花木,图中阴影部分铺上草坪. AP段栽种花木费用是每米3a元,CP段栽种花木费用是每米2a元,其中a是正常数.设
,在边BC上选一点P. 沿着AP和CP重新栽种花木,图中阴影部分铺上草坪. AP段栽种花木费用是每米3a元,CP段栽种花木费用是每米2a元,其中a是正常数.设![]() .
.
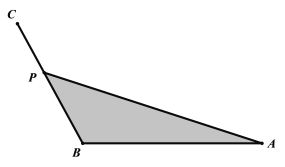
(1)求栽种花木费用y关于θ的函数表达式;
(2)求![]() 的值,使得栽种花木费用y最小.
的值,使得栽种花木费用y最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第三届移动互联创新大赛,于2017年3月~10月期间举行,为了选出优秀选手,某高校先在计算机科学系选出一种子选手![]() ,再从全校征集出3位志愿者分别与
,再从全校征集出3位志愿者分别与![]() 进行一场技术对抗赛,根据以往经验,
进行一场技术对抗赛,根据以往经验, ![]() 与这三位志愿者进行比赛一场获胜的概率分别为
与这三位志愿者进行比赛一场获胜的概率分别为![]() ,且各场输赢互不影响.
,且各场输赢互不影响.
(1)求甲恰好获胜两场的概率;
(2)求甲获胜场数的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
在![]() 中,内角A,B,C的对边分别为a,b,c,且满足________________,
中,内角A,B,C的对边分别为a,b,c,且满足________________,![]()
![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com