
设函数f(x)=xex,则( ).
A.x=1为f(x)的极大值点
B.x=1为f(x)的极小值点
C.x=-1为f(x)的极大值点
D.x=-1为f(x)的极小值点
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:填空题
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是________(写出所有正确命题的编号).

①当0<CQ< 时,S为四边形;
时,S为四边形;
②当CQ= 时,S为等腰梯形;
时,S为等腰梯形;
③当 <CQ<1时,S为六边形;
<CQ<1时,S为六边形;
④当CQ=1时,S的面积为 .
.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-3-2练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c,且2cos2 cos B-sin(A-B)sin B+cos(A+C)=-
cos B-sin(A-B)sin B+cos(A+C)=-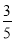 .
.
(1)求cos A的值;
(2)若a=4 ,b=5,求向量
,b=5,求向量 在
在 方向上的投影.
方向上的投影.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-3-1练习卷(解析版) 题型:选择题
已知ω>0,函数f(x)=sin  在
在 上单调递减,则ω的取值范围是( ).
上单调递减,则ω的取值范围是( ).
A. 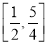 B.
B.  C.
C. 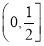 D.(0,2]
D.(0,2]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(解析版) 题型:填空题
设直线x=t,与函数f(x)=x2,g(x)=ln x的图象分别交于点M,N,则当|MN|达到最小时t的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(解析版) 题型:解答题
设函数f(x)=ax2+bx+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的零点;
(2)若对任意b∈R,函数f(x)恒有两个不同零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(解析版) 题型:选择题
根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为f(x)= (A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是 ( ).
(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是 ( ).
A.75,25 B.75,16 C.60,25 D.60,16
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(解析版) 题型:填空题
设0≤α≤π,不等式8x2-(8sin α)x+cos 2α≥0对x∈R恒成立,则α的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习真题感悟选修4练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,若l: (t为参数)过椭圆C:
(t为参数)过椭圆C: (φ为参数)的右顶点,则常数a的值为________.
(φ为参数)的右顶点,则常数a的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com