
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴非负半轴建立平面直角坐标系,直线
轴非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为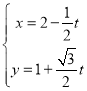 (
(![]() 为参数).
为参数).
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)在(1)中,设曲线![]() 经过伸缩变换
经过伸缩变换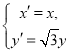 得到曲线
得到曲线![]() ,设曲线
,设曲线![]() 上任意一点为
上任意一点为![]() ,当点
,当点![]() 到直线
到直线![]() 的距离取最大值时,求此时点
的距离取最大值时,求此时点![]() 的直角坐标.
的直角坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 可将曲线
可将曲线![]() 的极坐标方程化为直角坐标方程,在直线
的极坐标方程化为直角坐标方程,在直线![]() 的参数方程中消去参数
的参数方程中消去参数![]() 可将直线
可将直线![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(2)利用伸缩变换求得曲线![]() 的普通方程,进而可得出曲线
的普通方程,进而可得出曲线![]() 的参数方程,设点
的参数方程,设点![]() ,利用点到直线的距离公式结合辅助角公式、正弦函数的有界性可求得点
,利用点到直线的距离公式结合辅助角公式、正弦函数的有界性可求得点![]() 到直线
到直线![]() 的距离的最大值,并求出对应的点
的距离的最大值,并求出对应的点![]() 的坐标.
的坐标.
(1)将曲线![]() 的极坐标方程化为
的极坐标方程化为![]() ,由
,由![]() ,
,
所以,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
在直线![]() 的参数方程中消去参数
的参数方程中消去参数![]() 得
得![]() ,
,
所以,直线![]() 的普通方程为
的普通方程为![]() ;
;
(2)由伸缩变换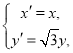 得
得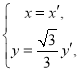 带入圆的方程
带入圆的方程![]() 得
得![]() ,
,
化简得曲线![]() ,其参数方程为
,其参数方程为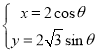 (
(![]() 为参数,且
为参数,且![]() ),
),
设点![]() ,
,
点![]() 到直线
到直线![]() 距离为:
距离为:
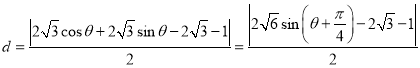 ,
,
![]() ,则
,则![]() ,所以,当
,所以,当![]() 时,即当
时,即当![]() 时,
时,
![]() 取最大值,即
取最大值,即![]() ,
,
此时,点![]() 的坐标为
的坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】孙子定理是中国古代求解一次同余式组的方法,是数论中一个重要定理,最早可见于中国南北朝时期的数学著作《孙子算经》,![]() 年英国来华传教士伟烈亚力将其问题的解法传至欧洲,
年英国来华传教士伟烈亚力将其问题的解法传至欧洲,![]() 年英国数学家马西森指出此法符合
年英国数学家马西森指出此法符合![]() 年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将
年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将![]() 至
至![]() 这
这![]() 个整数中能被
个整数中能被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】鱼卷是泉州十大名小吃之一,不但本地人喜欢,而且深受外来游客的赞赏.小张从事鱼卷生产和批发多年,有着不少来自零售商和酒店的客户当地的习俗是农历正月不生产鱼卷,客户正月所需要的鱼卷都会在上一年农历十二月底进行一次性采购小张把去年年底采购鱼卷的数量x(单位:箱)在![]() 的客户称为“熟客”,并把他们去年采购的数量制成下表:
的客户称为“熟客”,并把他们去年采购的数量制成下表:
采购数x |
|
|
|
|
|
客户数 | 10 | 10 | 5 | 20 | 5 |
(1)根据表中的数据作出频率分布直方图,并估计采购数在168箱以上(含168箱)的“熟客”人数;
(2)若去年年底“熟客”们采购的鱼卷数量占小张去年年底总的销售量的![]() ,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);
,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);
(3)由于鱼卷受到游客们的青睐,小张做了一份市场调查,决定今年年底是否在网上出售鱼卷,若不在网上出售鱼卷,则按去年的价格出售,每箱利润为20元,预计销售量与去年持平;若在网上出售鱼卷,则需把每箱售价下调2至5元,且每下调m元(![]() )销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.
)销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() ,以坐标原点O为极点,
,以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足|
于点M,点N为射线OM上的点,满足| ![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(1)①设动点![]() ,记
,记![]() 是直线
是直线![]() 的向上方向的单位方向向量,且
的向上方向的单位方向向量,且![]() ,以t为参数求直线
,以t为参数求直线![]() 的参数方程
的参数方程
②求曲线C的极坐标方程并化为直角坐标方程;
(2)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
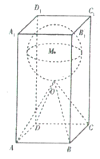
【题目】在日常生活中,石子是我们经常见到的材料,比如在各种建筑工地或者建材市场上常常能看到堆积如山的石子,它的主要成分是碳酸钙.某雕刻师计划在底面边长为2m、高为4m的正四棱柱形的石料![]() 中,雕出一个四棱锥
中,雕出一个四棱锥![]() 和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中
和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中![]() ,石料的密度
,石料的密度![]() ,质量
,质量![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面ABB1A1是边长为2的菱形,且CA=CB1.
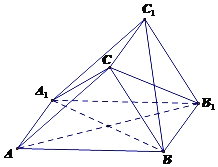
(1)证明:面CBA1⊥面CB1A;
(2)若∠BAA1=60°,A1C=BC=BA1,求点C到平面A1BC1的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com